Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Disphenoid"

(→‎Main)
(→‎Angular defects at two vertices and pare of opposite edges)
Line 137: Line 137:
 
The triples of points  <math>A_1, B, C_1</math> and  <math>B_1, A, C_1</math> are collinear. <math>A_1C = B_1C = CD \implies C</math> lies on bisector of segment <math>A_1B_1.</math>
 
The triples of points  <math>A_1, B, C_1</math> and  <math>B_1, A, C_1</math> are collinear. <math>A_1C = B_1C = CD \implies C</math> lies on bisector of segment <math>A_1B_1.</math>
  
−
1. Let the edges <math>AB</math> and <math>CD</math> are equal.
+
Case 1. Let the edges <math>AB</math> and <math>CD</math> are equal.
  
 
<math>AB</math> is the midsegment <math>\triangle A_1C_1B_1 \implies A_1B_1 = 2AB.</math>
 
<math>AB</math> is the midsegment <math>\triangle A_1C_1B_1 \implies A_1B_1 = 2AB.</math>
Line 145: Line 145:
 
the sum of the plane angles at vertices <math>C</math> is equal to <math>180^\circ \implies ABCD</math> is disphenoid.
 
the sum of the plane angles at vertices <math>C</math> is equal to <math>180^\circ \implies ABCD</math> is disphenoid.
  
−
2. The edges other than <math>AB</math> and <math>CD</math> are equal. WLOG, <math>AC = BD.</math>
+
Case 2. The edges other than <math>AB</math> and <math>CD</math> are equal. WLOG, <math>AC = BD.</math>
 
<cmath>A_1B = C_1B = BD = AC = \frac{A_1C_1}{2}.</cmath>
 
<cmath>A_1B = C_1B = BD = AC = \frac{A_1C_1}{2}.</cmath>
 
Note that in the process of constructing the development onto the plane <math>ABC,</math> the image of the face <math>ABD</math> and the face <math>ABC</math> are in different half-planes of the line <math>AB.</math>
 
Note that in the process of constructing the development onto the plane <math>ABC,</math> the image of the face <math>ABD</math> and the face <math>ABC</math> are in different half-planes of the line <math>AB.</math>

Revision as of 05:01, 16 August 2024

Disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles.

Main

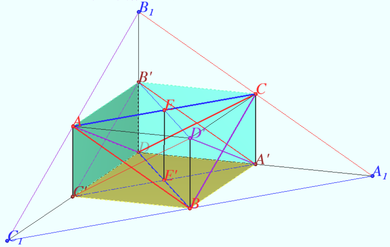
Disphenoid -parallelepiped.png

a) A tetrahedron $ABCD$ is a disphenoid iff $AB = CD, AC = BD, AD = BC.$

b) A tetrahedron is a disphenoid iff its circumscribed parallelepiped is right-angled.

c) Let $AB = a, AC = b, AD = c.$ The squares of the lengths of sides its circumscribed parallelepiped and the bimedians are: \[AB'^2 = l^2 = \frac {- a^2+b^2+c^2}{2}, AC'^2 = m^2 = \frac {a^{2}-b^{2}+c^{2}}{2},\] \[AD'^2 = n^2 = \frac {a^{2}+b^{2}-c^{2}}{2}\] The circumscribed sphere has radius (the circumradius): $R=\sqrt {\frac {a^2+b^2+c^2}{8}}.$

The volume of a disphenoid is: \[V= \frac {lmn}{3} = \sqrt {\frac {(a^2+b^2-c^2)(a^2-b^2+c^2)(-a^{2}+b^{2}+c^{2})}{72}}\] Each height of disphenoid $ABCD$ is $h=\frac {3V}{[ABC]},$ the inscribed sphere has radius: $r=\frac {3V}{4[ABC]},$ where $[ABC]$ is the area of $\triangle ABC.$

Proof

a) $AB \ne BC, AB \ne AD, \triangle ABC = \triangle BAD = \triangle CDA = \triangle DCB.$

$AB \ne AD, AB \ne BD$ because in $\triangle ABD$ there is no equal sides.

Let consider $\triangle BCD.$

$BD \ne AB, BC \ne AB,$ but one of sides need be equal $AB,$ so $AB = CD \implies AC = BD, AD = BC.$

b) Any tetrahedron can be assigned a parallelepiped by drawing a plane through each edge of the tetrahedron parallel to the opposite edge.

$AB = CD = C'D' \implies AD'BC'$ is parallelogram with equal diagonals, i.e. rectangle.

Similarly, $AB'CD'$ and $AB'DC'$ are rectangles.

If $AD'BC'$ is rectangle, then $AB = C'D' = CD.$

Similarly, $AC = BD, AD = BC \implies ABCD$ is a disphenoid.

c) $AB^2 = a^2 = AC'^2 + BC'^2 = m^2 + AD'^2 = m^2 + n^2.$

Similarly, $AC^2 = b^2 = l^2 + n^2, AD^2 = c^2 = l^2 + m^2 \implies 2(l^2 + m^2 + n^2) = a^2 + b^2 + c^2 \implies$ \[l^2 = l^2 + m^2 + n^2 - (m^2 + n^2) = \frac {a^2 + b^2 + c^2}{2} - a^2 = \frac {-a^2 + b^2 + c^2}{2}.\]

Similarly, $m^2 = \frac {a^2 - b^2 + c^2}{2}, n^2 = \frac {a^2 + b^2 - c^2}{2}.$

Let $E$ be the midpoint $AC$, $E'$ be the midpoint $BD \implies$

$EE' = AC' = m = \sqrt {\frac {a^2 - b^2 + c^2}{2}}$ is the bimedian of $AC$ and $BD.$ \[EE' || AC' \implies EE' \perp AC, EE' \perp BD.\]

The circumscribed sphere of $ABCD$ is the circumscribed sphere of $AB'CD'C'DA'C,$ so it is \[\frac {AA'}{2} = \sqrt {\frac {a^2+b^2+c^2}{8}}.\]

The volume of a disphenoid is third part of the volume of $AB'CD'C'DA'C,$ so: \[V= \frac {l \cdot m \cdot n}{3} = \sqrt {\frac {(a^2+b^2-c^2)(a^2-b^2+c^2)(-a^{2}+b^{2}+c^{2})}{72}}.\] The volume of a disphenoid is $V = \frac {1}{3} h [ABC] \implies h = \frac{3V}{[ABC]},$ where $h$ is any height.

The inscribed sphere has radius $r = \frac{h}{4}.$ \[72 V^2 = (a^2+b^2-c^2) \cdot (a^2-b^2+c^2) \cdot (-a^2+b^2+c^2) =-a^6+a^4 b^2+a^4 c^2+a^2 b^4+a^2 c^4-b^6+b^4 c^2+b^2 c^4-c^6 -2a^2 b^2 c^2,\] \[16 [ABC]^2 = (a+b+c)(a+b-c)(a-b+c)(-a+b+c) = -a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4,\] \[8 R^2 = a^2+b^2+c^2,\] \[128 R^2 [ABC]^2 = -a^6+a^4 b^2+a^4 c^2+a^2 b^4 +a^2 c^4-b^6+b^4 c^2+b^2 c^4-c^6 + 6a^2 b^2 c^2.\]

Therefore $16 R^2 [ABC]^2 = a^2 b^2 c^2 + 9 V^2.$

Corollary

$ABC$ is acute-angled triangle, becouse $l^2 = -a^2+b^2 +c^2 >0, m^2 = a^2-b^2+c^2 > 0, n^2 = a^2+b^2-c^2 > 0.$

vladimir.shelomovskii@gmail.com, vvsss

Constructing

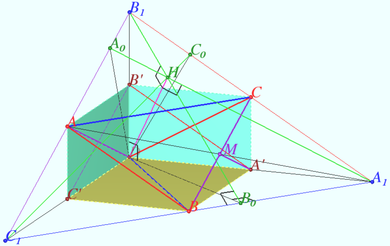
Disphenoid -parallelepiped A.png

Let triangle $ABC$ be given. Сonstruct the disphenoid $ABCD.$

Solution

Let $\triangle A_1B_1C_1$ be the anticomplementary triangle of $\triangle ABC, M$ be the midpoint $BC.$

Then $M$ is the midpoint of segment $AA_1 \implies$

$2MA' = AD, MA' || AD \implies A'$ is the midpoint $A_1D.$

Similarly, $B'$ is the midpoint $B_1D, C'$ is the midpoint $C_1D.$

So, $\angle A_1DB_1 = \angle B_1DC_1 = \angle C_1DA_1 = 90^\circ.$

Let $A_1A_0, B_1B_0, C_1C_0$ be the altitudes of $\triangle A_1B_1C_1, H$ be the orthocenter of $\triangle A_1B_1C_1 \implies DH \perp ABC.$

To construct the disphenoid $ABCD$ using given triangle $ABC$ we need:

1) Construct $\triangle A_1B_1C_1,$ the anticomplementary triangle of $\triangle ABC,$

2) Find the orthocenter $H$ of $\triangle A_1B_1C_1.$

3) Construct the perpendicular from point $H$ to plane $ABC.$

4) Find the point $D$ in this perpendicular such that $AD = BC.$


vladimir.shelomovskii@gmail.com, vvsss

Properties and signs of disphenoid

Three sums of the plane angles

The sums of the plane angles (the angular defects) at any three vertices of the tetrahedron are equal to $180^\circ$ iff the tetrahedron is disphenoid.

Proof

The sum of the all plane angles of the tetrahedron is the sum of plane angles of four triangles, so the sum of plane angles of fourth vertice is $180^\circ.$

The development of the tetrahedron $ABCD$ on the plane $ABC$ is a hexagon $A_1CB_1AC_1B.$

a) If the angular defect of vertex $C$ is $180^\circ,$ then angle \[\angle A_1CB_1 = \angle A_1CB + \angle BCA + \angle ACB_1 = \angle DCB + \angle BCA + \angle ACD = 180^\circ,\] so points $A_1, C,$ and $B_1$ are collinear.

Similarly, triples of points $A_1, B, C_1$ and $B_1, A, C_1$ are collinear.

The hexagon $A_1CB_1AC_1B$ is the triangle, where the points $A, B,$ and $C$ are the midpoints of sides $B_1C_1,A_1C_1,$ and $A_1B_1,$ respectively.

Consequently, $\triangle ABC = \triangle A_1CB = \triangle DCB.$

Similarly, all faces of the tetrahedron are equal. The tetrahedron is disphenoid.

b) If the tetrahedron is disphenoid, then any two of its adjacent faces form a parallelogram when developed.

Consequently, the development of the tetrahedron is a triangle, i.e. the sums of the plane angles at the vertices of the tetrahedron are equal to $180^\circ.$

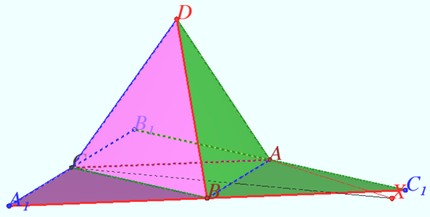
Angular defects at two vertices and pare of opposite edges

Disphenoid development.png

The tetrahedron is disphenoid if the sums of the plane angles (the angular defects) at any two vertices of the tetrahedron are equal to $180^\circ$ and any two opposite edges are equal.

Proof

Let the sums of the plane angles at vertices $A$ and $B$ be equal to $180^\circ.$

Consider the development of the tetrahedron on the plane of face $ABC.$

The triples of points $A_1, B, C_1$ and $B_1, A, C_1$ are collinear. $A_1C = B_1C = CD \implies C$ lies on bisector of segment $A_1B_1.$

Case 1. Let the edges $AB$ and $CD$ are equal.

$AB$ is the midsegment $\triangle A_1C_1B_1 \implies A_1B_1 = 2AB.$

$CD = AB \implies C$ is the midpoint of the segment $A_1B_1 \implies$

the sum of the plane angles at vertices $C$ is equal to $180^\circ \implies ABCD$ is disphenoid.

Case 2. The edges other than $AB$ and $CD$ are equal. WLOG, $AC = BD.$ \[A_1B = C_1B = BD = AC = \frac{A_1C_1}{2}.\] Note that in the process of constructing the development onto the plane $ABC,$ the image of the face $ABD$ and the face $ABC$ are in different half-planes of the line $AB.$

Accordingly, the image of the vertex $D$ of the face $ABD$ and the vertex $C$ are located on different sides of the line $AB.$

There are only two points on bisector of segment $A_1B_1$ such that distance from $A$ is equal to $BD.$

One of them is designated as $X$ on the diagram. It lies at the same semiplane $AB$ as $C_1$ which is impossible.

The second is the midpoint of segment $A_1B_1 \implies$

the sum of the plane angles at vertices $C$ is equal to $180^\circ \implies ABCD$ is disphenoid.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Disphenoid&oldid=225117"