Difference between revisions of "DVI exam"
(→2022 221 problem 7) |
(→2022 221 problem 7) |
||
| Line 1: | Line 1: | ||
==2022 221 problem 7== | ==2022 221 problem 7== | ||
| − | [[File:MSU 2022 7.png| | + | [[File:MSU 2022 7.png|330px|right]] |
| + | [[File:MSU 2022 7a.png|330px|right]] | ||
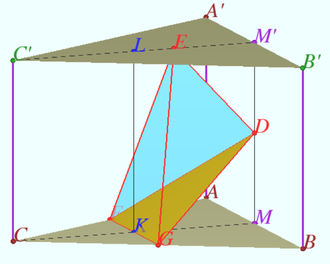
The volume of a triangular prism <math>ABCA'B'C'</math> with base <math>ABC</math> and side edges <math>AA', BB', CC'</math> is equal to <math>72.</math> Find the volume of the tetrahedron <math>DEFG,</math> where <math>D</math> is the centroid of the face <math>ABC'A', E</math> is the point of intersection of the medians of <math>\triangle A'B'C', F</math> is the midpoint of the edge <math>AC</math> and <math>G</math> is the midpoint of the edge <math>BC.</math> | The volume of a triangular prism <math>ABCA'B'C'</math> with base <math>ABC</math> and side edges <math>AA', BB', CC'</math> is equal to <math>72.</math> Find the volume of the tetrahedron <math>DEFG,</math> where <math>D</math> is the centroid of the face <math>ABC'A', E</math> is the point of intersection of the medians of <math>\triangle A'B'C', F</math> is the midpoint of the edge <math>AC</math> and <math>G</math> is the midpoint of the edge <math>BC.</math> | ||
| Line 14: | Line 15: | ||
<cmath>\frac {U}{V} = \frac {\frac {5}{72} CC' \cdot CM \cdot FG}{\frac{1}{3} CM \cdot FG \cdot CC'} = \frac {5}{24} \implies U = 15.</cmath> | <cmath>\frac {U}{V} = \frac {\frac {5}{72} CC' \cdot CM \cdot FG}{\frac{1}{3} CM \cdot FG \cdot CC'} = \frac {5}{24} \implies U = 15.</cmath> | ||
| − | An arbitrary prism is obtained from a regular one as a result of an affine transformation | + | An arbitrary prism is obtained from a regular one as a result of an affine transformation. |
| + | |||
| + | All points on the tetrahedron are defined affinely, which means that the volume ratio will be preserved. | ||
<i><b>Answer: 15.</b></i> | <i><b>Answer: 15.</b></i> | ||
Revision as of 04:44, 28 January 2024
2022 221 problem 7
The volume of a triangular prism 
with base 
and side edges 
is equal to 
Find the volume of the tetrahedron 
where 
is the centroid of the face 
is the point of intersection of the medians of 
is the midpoint of the edge 
and 
is the midpoint of the edge 
Solution
Let us consider the uniform triangular prism 
Let 
be the midpoint of 
be the midpoint of 
be the midpoint of 
be the midpoint of 
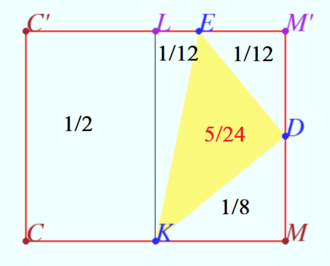
The area ![$[KED]$](http://latex.artofproblemsolving.com/f/b/a/fba57621447876aa5fd27d1e0dcafd32131a1bbd.png)
of 
in the sum with the areas of triangles ![$[KEL], [EDM'], [KDM]$](http://latex.artofproblemsolving.com/f/1/9/f19629b2cd5a7d03bc75888eb448b289d2031c3b.png)
is half the area of rectangle 
so
![\[\frac {[KED]}{[CC'M'M]} = \frac {1}{2} - \frac {1}{12}-\frac {1}{8} = \frac {5}{24}.\]](http://latex.artofproblemsolving.com/8/0/7/8070e8fa4c71175860e89cdd4de9080131b9ff5a.png)
![\[FG \perp ED, 2 FG = AB.\]](http://latex.artofproblemsolving.com/1/9/c/19c6c411904526c78dcffc0e15b5fb12f6765f30.png)
Denote the distance between these lines 
The volume of the tetrahedron is 
![\[\frac {ED \cdot X}{2} = \frac {5}{24} \cdot CC' \cdot CM \implies U =\frac{5}{24 \cdot 3} \cdot CC' \cdot CM \cdot FG.\]](http://latex.artofproblemsolving.com/b/a/8/ba85504fb9ccffaf3a58cf1ad5589e3b4c47a01c.png)
The volume of the prism is 
![\[\frac {U}{V} = \frac {\frac {5}{72} CC' \cdot CM \cdot FG}{\frac{1}{3} CM \cdot FG \cdot CC'} = \frac {5}{24} \implies U = 15.\]](http://latex.artofproblemsolving.com/0/3/d/03d69d7f37bf257dde5affef97474c1bea89cdaa.png)
An arbitrary prism is obtained from a regular one as a result of an affine transformation.
All points on the tetrahedron are defined affinely, which means that the volume ratio will be preserved.
Answer: 15.
2022 222 problem 7
![\[r = 0.5, h = 3/2, KM = \frac {\sqrt{3}}{2},\]](http://latex.artofproblemsolving.com/1/d/c/1dca112ae88f73b3097142899ae597d9184f3a30.png)
![\[AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha},\]](http://latex.artofproblemsolving.com/2/b/c/2bc88738c2efa898feb0c22b93dc8754aa27f8d8.png)
![\[AM + BM = AB \implies\]](http://latex.artofproblemsolving.com/6/6/b/66bd3dd3f4588d2579c1569d2c36491417e20a8c.png)
![\[\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.\]](http://latex.artofproblemsolving.com/a/d/9/ad94bbf8346d00722305ab7c3dca276520748cb6.png)
