Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 15"
| Line 2: | Line 2: | ||
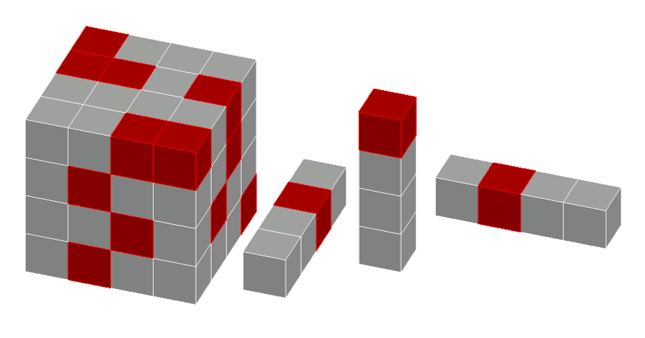
A <math>4\times4\times4</math> [[cube (geometry) | cube]] is composed of <math>64</math> unit cubes. The faces of <math>16</math> unit cubes are colored red. An arrangement of the cubes is "intriguing" if there is exactly <math>1</math> red unit cube in every <math>1\times1\times4</math> rectangular box composed of <math>4</math> unit cubes. Determine the number of "intriguing" colorings. | A <math>4\times4\times4</math> [[cube (geometry) | cube]] is composed of <math>64</math> unit cubes. The faces of <math>16</math> unit cubes are colored red. An arrangement of the cubes is "intriguing" if there is exactly <math>1</math> red unit cube in every <math>1\times1\times4</math> rectangular box composed of <math>4</math> unit cubes. Determine the number of "intriguing" colorings. | ||
| − | [[Image: | + | [[Image:AIME_2006_P15a.png]] |
==Solution== | ==Solution== | ||
Revision as of 19:38, 22 November 2023
Contents
Problem
A ![]() cube is composed of
cube is composed of ![]() unit cubes. The faces of
unit cubes. The faces of ![]() unit cubes are colored red. An arrangement of the cubes is "intriguing" if there is exactly
unit cubes are colored red. An arrangement of the cubes is "intriguing" if there is exactly ![]() red unit cube in every
red unit cube in every ![]() rectangular box composed of
rectangular box composed of ![]() unit cubes. Determine the number of "intriguing" colorings.
unit cubes. Determine the number of "intriguing" colorings.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
See Also
| Mock AIME 2 2006-2007 (Problems, Source) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||