Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 12B Problems/Problem 20"

(→‎Solution 3(coord bash))
Line 5: Line 5:
  
 
==Solution 1==
 
==Solution 1==
 +
 +
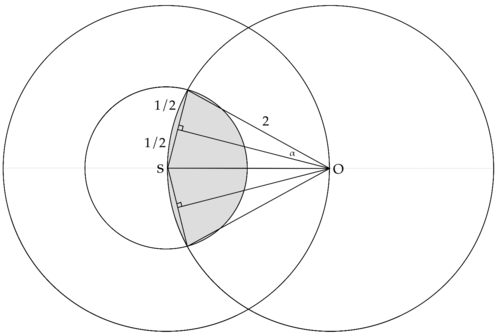
[[File:2023AMC12BP20.png|center|500px]]
 +
 +
(Writing in progress......)
 +
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 +
 +
==Solution 2==
 
Denote by <math>A_i</math> the position after the <math>i</math>th jump.
 
Denote by <math>A_i</math> the position after the <math>i</math>th jump.
 
Thus, to fall into the region centered at <math>A_0</math> and with radius 1, <math>\angle A_2 A_1 A_0 < 2 \arcsin \frac{1/2}{2} = 2 \arcsin \frac{1}{4}</math>.
 
Thus, to fall into the region centered at <math>A_0</math> and with radius 1, <math>\angle A_2 A_1 A_0 < 2 \arcsin \frac{1/2}{2} = 2 \arcsin \frac{1}{4}</math>.
Line 17: Line 25:
  
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
−
 
−
==Solution 2==
 
−
 
−
(Diagram in progress......)
 
−
(Writing in progress......)
 
−
 
−
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
  
 
==Solution 3(coord bash)==
 
==Solution 3(coord bash)==

Revision as of 22:25, 15 November 2023

Problem

Cyrus the frog jumps 2 units in a direction, then 2 more in another direction. What is the probability that he lands less than 1 unit away from his starting position?

$\textbf{(A)}~\frac{1}{6}\qquad\textbf{(B)}~\frac{1}{5}\qquad\textbf{(C)}~\frac{\sqrt{3}}{8}\qquad\textbf{(D)}~\frac{\arctan \frac{1}{2}}{\pi}\qquad\textbf{(E)}~\frac{2\arcsin \frac{1}{4}}{\pi}$

Solution 1

2023AMC12BP20.png

(Writing in progress......)

~isabelchen

Solution 2

Denote by $A_i$ the position after the $i$th jump. Thus, to fall into the region centered at $A_0$ and with radius 1, $\angle A_2 A_1 A_0 < 2 \arcsin \frac{1/2}{2} = 2 \arcsin \frac{1}{4}$.

Therefore, the probability is \[ \frac{2 \cdot 2 \arcsin \frac{1}{4}}{2 \pi} = \boxed{\textbf{(E) } \frac{2 \arcsin \frac{1}{4}}{\pi}}. \]

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 3(coord bash)

Let the orgin be the starting point of frog. Then, WLOG assume that after the first jump, it is at the point (2,0). Then, the range of all possible places the frog can jump to at its second jump is the circle with equation $(x-2)^2+y^2=2^2$.If it landed $1$ unit within its starting point (the orgin), then it is inside the circle $x^2+y^2=1$. We clearly want the intersection point. So we're tring to solve the system of equations $x^2+y^2=1$ and $(x-2)^2+y^2=2^2$. We have $x=\frac{1}{4}$, so $y=\pm\frac{\sqrt{15}}{4}$. (writing continueing) ~ddk001

See Also

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_12B_Problems/Problem_20&oldid=203781"