Difference between revisions of "Symmetry"
(→Composition of symmetries 1) |
(→Symmetry with respect angle bisectors 2) |
||
| Line 38: | Line 38: | ||
Symilarly, <cmath>BA' = EB' \implies EB' = DB'. \blacksquare.</cmath> | Symilarly, <cmath>BA' = EB' \implies EB' = DB'. \blacksquare.</cmath> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| − | ==Symmetry with respect angle bisectors | + | ==Symmetry with respect angle bisectors 1== |
[[File:Bisectors 3.png|350px|right]] | [[File:Bisectors 3.png|350px|right]] | ||
The bisector <math>BI</math> intersect the incircle <math>\omega</math> of the triangle <math>\triangle ABC</math> at the point <math>K, B' = \omega \cap AC.</math> | The bisector <math>BI</math> intersect the incircle <math>\omega</math> of the triangle <math>\triangle ABC</math> at the point <math>K, B' = \omega \cap AC.</math> | ||
| Line 51: | Line 51: | ||
Similarly <math>\overset{\Large\frown} {KA'} = \overset{\Large\frown} {EB'} \implies </math> | Similarly <math>\overset{\Large\frown} {KA'} = \overset{\Large\frown} {EB'} \implies </math> | ||
<cmath> \overset{\Large\frown} {DB'} = \overset{\Large\frown} {EB'} \blacksquare.</cmath> | <cmath> \overset{\Large\frown} {DB'} = \overset{\Large\frown} {EB'} \blacksquare.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==Symmetry with respect angle bisectors 2== | ||
| + | [[File:Bisectors 3.png|350px|right]] | ||
| + | Given the triangle <math>\triangle ABC, \omega</math> is the incircle, <math>I</math> is the incenter, <math>B' = \omega \cap AC, C' = \omega \cap AB.</math> | ||
| + | Let <math>D</math> be the point on sideline <math>BC.</math> | ||
| + | Points <math>E</math> and <math>F</math> are symmetrical to point <math>D</math> with respect to the lines <math>BI</math> and <math>CI,</math> respectively. The line <math>\ell \perp EF</math> contains point <math>I.</math> | ||
| + | Prove that <math>M = B'C' \cap \ell</math> is the midpoint <math>EF.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | The segment <math>EC'</math> is symmetric to <math>DA'</math> with respect to <math>BI,</math> the segment <math>FB'</math> is symmetric to <math>DA'</math> with respect to <math>CI.</math> So <math>EC' = FB'.</math> | ||
| + | Similarly <math>ID = IE = IF \implies \ell \cap EF</math> at midpoint <math>EF.</math> | ||
| + | |||
| + | <cmath>AB' = AC' \implies \angle AB'C' = \angle AC'B'.</cmath> | ||
| + | <math>\angle MB'F = \angle AB'C</math> or <math>\angle MB'F + \angle AB'C = 180^\circ \implies \sin \angle ECM = \sin \angle MB'F.</math> | ||
| + | <math>\angle EMC' = \angle B'MF</math> or <math>\angle EMC' + \angle B'MF = 180^\circ \implies \sin \angle EMC = \sin \angle B'MF.</math> | ||
| + | We use the Law of Sines and get: | ||
| + | <cmath>\frac {ME}{\sin {EC'M}} : \frac {MF}{\sin {MB'F}} = \frac {EC'}{\sin {EMC'}} : \frac {BF}{\sin {B'MF}} \implies \frac {ME}{MF} = \frac {EC'}{BF} = 1. \blacksquare</cmath> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 13:29, 29 August 2023
A proof utilizes symmetry if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent to each other that all three angles are equal, you only need to prove that if ![]() then
then ![]() the other cases hold by symmetry because the steps are the same.
the other cases hold by symmetry because the steps are the same.
Contents
Hidden symmetry
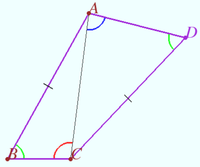
Let the convex quadrilateral ![]() be given.
be given.
![]()
Prove that ![]()
Proof
Let ![]() be bisector
be bisector ![]()
Let point ![]() be symmetric
be symmetric ![]() with respect
with respect ![]()
![]()
![]() is isosceles.
is isosceles.
Therefore ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
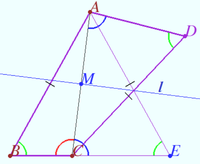
Symmetry with respect angle bisectors
Given the triangle ![]() is the incircle,
is the incircle, ![]() is the incenter,
is the incenter, ![]()
Points ![]() and
and ![]() are symmetrical to point
are symmetrical to point ![]() with respect to the lines containing the bisectors
with respect to the lines containing the bisectors ![]() and
and ![]() respectively.
respectively.
Prove that ![]() is the midpoint
is the midpoint ![]()
Proof
![]() Denote
Denote ![]()
The tangents from point ![]() to
to ![]() are equal
are equal ![]()
Point ![]() is symmetrical to point
is symmetrical to point ![]() with respect
with respect ![]() is symmetrical to segment
is symmetrical to segment ![]()
Symilarly, ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
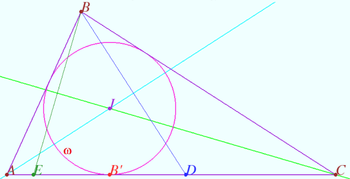
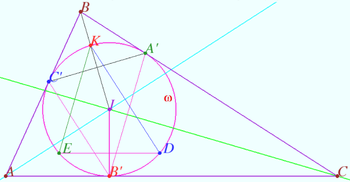
Symmetry with respect angle bisectors 1
The bisector ![]() intersect the incircle
intersect the incircle ![]() of the triangle
of the triangle ![]() at the point
at the point ![]() The point
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() the point
the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() Prove that
Prove that ![]() is the bisector of the segment
is the bisector of the segment ![]()
Proof
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() Similarly
Similarly ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
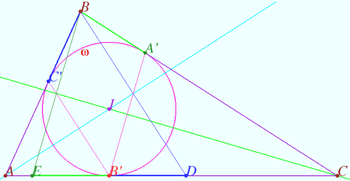
Symmetry with respect angle bisectors 2
Given the triangle ![]() is the incircle,
is the incircle, ![]() is the incenter,
is the incenter, ![]() Let
Let ![]() be the point on sideline
be the point on sideline ![]() Points
Points ![]() and
and ![]() are symmetrical to point
are symmetrical to point ![]() with respect to the lines
with respect to the lines ![]() and
and ![]() respectively. The line
respectively. The line ![]() contains point
contains point ![]() Prove that
Prove that ![]() is the midpoint
is the midpoint ![]()
Proof
The segment ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() the segment
the segment ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() So
So ![]() Similarly
Similarly ![]() at midpoint
at midpoint ![]()
![]()
![]() or
or ![]()
![]() or
or ![]() We use the Law of Sines and get:
We use the Law of Sines and get:
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Composition of symmetries
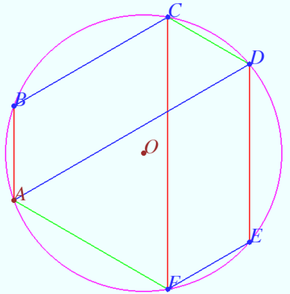
Let the inscribed convex hexagon ![]() be given,
be given,
![]() Prove that
Prove that ![]()
Proof
Denote ![]() the circumcenter of
the circumcenter of ![]()
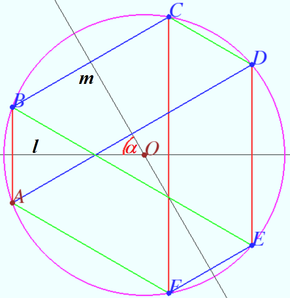
![]() the common bisector
the common bisector ![]() the common bisector
the common bisector ![]()
![]() the smaller angle between lines
the smaller angle between lines ![]() and
and ![]()
![]() is the symmetry with respect axis
is the symmetry with respect axis ![]() is the symmetry with respect axis
is the symmetry with respect axis ![]()
It is known that the composition of two axial symmetries with non-parallel axes is a rotation centered at point of intersection of the axes at twice the angle from the axis of the first symmetry to the axis of the second symmetry.
![]()
![]()
![]() Therefore
Therefore ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
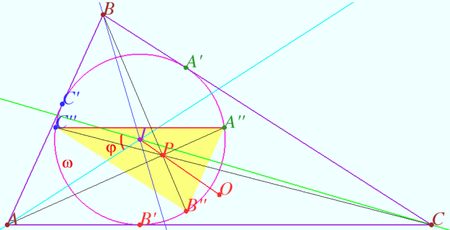
Composition of symmetries 1
Let the triangle ![]() be given.
be given.
![]() is the incircle,
is the incircle, ![]() is the incenter,
is the incenter, ![]() is the circumcenter of
is the circumcenter of ![]()
![]() The point
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
Prove: a)![]()
b) ![]()
Proof
a) Denote ![]() the smaller angle between
the smaller angle between ![]() and
and ![]()
![]() is the symmetry with respect axis
is the symmetry with respect axis ![]() is the symmetry with respect axis
is the symmetry with respect axis ![]()
![]() counterclockwise direction.
counterclockwise direction.
![]() clockwise direction.
clockwise direction.
Therefore ![]() is parallel to tangent line for
is parallel to tangent line for ![]() at point
at point ![]()
b) ![]() is homothetic to
is homothetic to ![]()
![]() is the circumcenter of
is the circumcenter of ![]()
The center of the homothety lies on the line passing through the circumcenters of the triangles. ![]()
vladimir.shelomovskii@gmail.com, vvsss