Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Barycentric coordinates"
Line 8: Line 8:
  
 
[[File:Barycentric_901.gif]]
 
[[File:Barycentric_901.gif]]
 +
 +
==Useful formulas==
 +
Let the triangle <math>\triangle ABC</math> be a given triangle, <math>a, b, c</math> be the lengths of <math>BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.</math>
 +
 +
We use the following Conway symbols:
 +
 +
<math>s = \frac {a+b+c}{2}</math> is semiperimeter, <math>2S </math> is  twice the area of <math>\triangle ABC,</math>
 +
 +
<math>r^2 = \frac {(s-a)(s-b)(s-c)}{s},</math> where <math>r</math> is the inradius, <math>R = \frac {abc}{2 \cdot 2S}</math> is the circumradius,
 +
 +
<math>\cos \omega = \frac {a^2 + b^2 +c^2}{2 \cdot 2S}</math> is the cosine of the Brocard angle.
 +
 +
<cmath>S_A = bc \cos \alpha = \frac{b^2+c^2-a^2}{2}, S_B = ac \cos \beta =\frac{a^2 +c^2-b^2}{2}, S_C = ab \cos \gamma = \frac {a^2+b^2-c^2}{2}.</cmath>
 +
For any point in the plane  <math>ABC</math> there are barycentric coordinates:
 +
<cmath>x \cdot \vec {XA} + y \cdot \vec {YB} + z \cdot \vec {XC} = \vec {0},</cmath>
 +
<cmath>\vec X = \frac {x \cdot \vec {A} + y \cdot \vec {B} + z \cdot \vec {C}}{x+y+z}.</cmath>
 +
The normalized (absolute) barycentric coordinates NBC satisfy the condition <math>x + y + z = 1,</math> they are uniquely determined:
 +
<cmath>x = \frac{[\vec {XB},\vec {XC}]}{\sigma}, y = \frac{[\vec {XC},\vec {XA}]}{\sigma}, z = \frac{[\vec {XA},\vec {XB}]}{\sigma},  \sigma = [\vec {XB},\vec {XC}] + [\vec {XC},\vec {XA}] + [\vec {XA},\vec {XB}] .</cmath>
 +
Triangle vertices <math>A = (1:0:0), B = (0:1:0), C = (0:0:1).</math>
 +
 +
The barycentric coordinates of a point do not change under an affine transformation.
 +
 +
The straight line in barycentric coordinates (BC) is given by the equation <math>kx + ly + mz = 0.</math>
 +
 +
The lines given in the BC by the equations <math>k_1x + l_1y + m_1z = 0</math> and <math>k_2x + l_2y + m_2z = 0</math> intersect at the point
 +
<cmath>(l_1m_2 – m_1l_2 : m_1k_2-k_1m_2 : k_1l_2-l_1k_2).</cmath>
 +
 +
These lines are parallel iff <math>l_1m_2 – m_1l_2 + m_1k_2-k_1m_2 + k_1l_2-l_1k_2 = 0.</math>
 +
 +
The sideline <math>BC</math> contains the points <math>B = (0:1:0), C = (0:0:1),</math> its equation is <math>x = 0.</math>
 +
 +
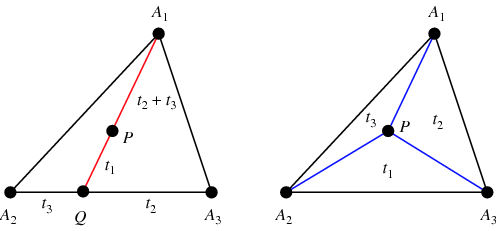
The line <math>AX, X = (k_1 :  l_1  :  m_1)</math> has equation <math>l_1z = m_1 y,</math> it intersects the sideline <math>BC</math> at the point <math>A_1 = (0 : l_1 : m_1), \frac {BA_1}{A_1C} = \frac {m_1}{l_1}.</math>
 +
 +
Iff <math>A_1 = (0 : l_1 : m_1), B_1 = (k_1  : 0 : m_1 ), C_1 = (k_1  : l_1  : 0),</math> then <math>AA_1 \cap BB_1 \cap CC_1 = (k_1  : l_1 : m_1 ).</math>
 +
 +
Let NBC of points <math>P</math> and <math>Q</math> be <math>P = (x_1 : y_1 : z_1), Q = (x_2 : y_2 : z_2).</math>
 +
 +
Then the square of distance  <cmath>|PQ|^2 = S_A \cdot (x_1 - x_2)^2 + S_B(y_1 - y_2)^2 + S_C(z_1 - z_2)^2.</cmath>
 +
<cmath>|PQ|^2 = - a^2 (y_1 - y_2)(z_1 - z_2) - b^2 (x_1 - x_2)(z_1 - z_2) - c^2 (x_1 - x_2)(y_1 - y_2).</cmath>

Revision as of 12:31, 25 August 2023

This can be used in mass points. http://mathworld.wolfram.com/BarycentricCoordinates.html This article is a stub. Help us out by expanding it.

Barycentric coordinates are triples of numbers $(t_1,t_2,t_3)$ corresponding to masses placed at the vertices of a reference triangle $\Delta{A_1}{A_2}{A_3}$. These masses then determine a point $P$, which is the geometric centroid of the three masses and is identified with coordinates $(t_1,t_2,t_3)$. The vertices of the triangle are given by $(1,0,0)$, $(0,1,0)$, and $(0,0,1)$. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).

The Central NC Math Group published a lecture concerning this topic at https://www.youtube.com/watch?v=KQim7-wrwL0 if you would like to view it.

Barycentric 901.gif

Useful formulas

Let the triangle $\triangle ABC$ be a given triangle, $a, b, c$ be the lengths of $BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.$

We use the following Conway symbols:

$s = \frac {a+b+c}{2}$ is semiperimeter, $2S$ is twice the area of $\triangle ABC,$

$r^2 = \frac {(s-a)(s-b)(s-c)}{s},$ where $r$ is the inradius, $R = \frac {abc}{2 \cdot 2S}$ is the circumradius,

$\cos \omega = \frac {a^2 + b^2 +c^2}{2 \cdot 2S}$ is the cosine of the Brocard angle.

\[S_A = bc \cos \alpha = \frac{b^2+c^2-a^2}{2}, S_B = ac \cos \beta =\frac{a^2 +c^2-b^2}{2}, S_C = ab \cos \gamma = \frac {a^2+b^2-c^2}{2}.\] For any point in the plane $ABC$ there are barycentric coordinates: \[x \cdot \vec {XA} + y \cdot \vec {YB} + z \cdot \vec {XC} = \vec {0},\] \[\vec X = \frac {x \cdot \vec {A} + y \cdot \vec {B} + z \cdot \vec {C}}{x+y+z}.\] The normalized (absolute) barycentric coordinates NBC satisfy the condition $x + y + z = 1,$ they are uniquely determined: \[x = \frac{[\vec {XB},\vec {XC}]}{\sigma}, y = \frac{[\vec {XC},\vec {XA}]}{\sigma}, z = \frac{[\vec {XA},\vec {XB}]}{\sigma}, \sigma = [\vec {XB},\vec {XC}] + [\vec {XC},\vec {XA}] + [\vec {XA},\vec {XB}] .\] Triangle vertices $A = (1:0:0), B = (0:1:0), C = (0:0:1).$

The barycentric coordinates of a point do not change under an affine transformation.

The straight line in barycentric coordinates (BC) is given by the equation $kx + ly + mz = 0.$

The lines given in the BC by the equations $k_1x + l_1y + m_1z = 0$ and $k_2x + l_2y + m_2z = 0$ intersect at the point \[(l_1m_2 – m_1l_2 : m_1k_2-k_1m_2 : k_1l_2-l_1k_2).\]

These lines are parallel iff $l_1m_2 – m_1l_2 + m_1k_2-k_1m_2 + k_1l_2-l_1k_2 = 0.$

The sideline $BC$ contains the points $B = (0:1:0), C = (0:0:1),$ its equation is $x = 0.$

The line $AX, X = (k_1 : l_1  : m_1)$ has equation $l_1z = m_1 y,$ it intersects the sideline $BC$ at the point $A_1 = (0 : l_1 : m_1), \frac {BA_1}{A_1C} = \frac {m_1}{l_1}.$

Iff $A_1 = (0 : l_1 : m_1), B_1 = (k_1  : 0 : m_1 ), C_1 = (k_1  : l_1  : 0),$ then $AA_1 \cap BB_1 \cap CC_1 = (k_1  : l_1 : m_1 ).$

Let NBC of points $P$ and $Q$ be $P = (x_1 : y_1 : z_1), Q = (x_2 : y_2 : z_2).$

Then the square of distance \[|PQ|^2 = S_A \cdot (x_1 - x_2)^2 + S_B(y_1 - y_2)^2 + S_C(z_1 - z_2)^2.\] \[|PQ|^2 = - a^2 (y_1 - y_2)(z_1 - z_2) - b^2 (x_1 - x_2)(z_1 - z_2) - c^2 (x_1 - x_2)(y_1 - y_2).\]

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Barycentric_coordinates&oldid=197437"