Difference between revisions of "Spiral similarity"
(→Remarkable point of spiral similarity) |
(→Remarkable point for pair of similar triangles) |
||
| Line 282: | Line 282: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
===Remarkable point for pair of similar triangles=== | ===Remarkable point for pair of similar triangles=== | ||
| − | [[File:Similar triangles.png| | + | [[File:Similar triangles.png|400px|right]] |
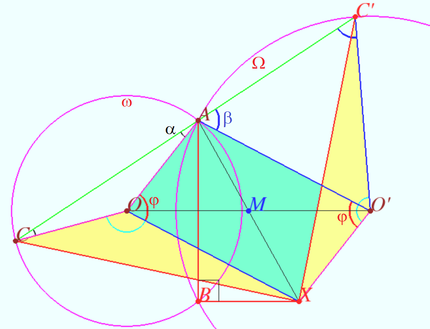
| − | Let <math>\triangle ACD \sim \triangle AC'D'.</math> Let the points <math>O</math> and <math>O'</math> be the circumcenters of <math>\omega (\triangle ACD</math> and <math>\Omega (\triangle AC'D').</math> | + | [[File:Similar triangles A.png|400px|right]] |
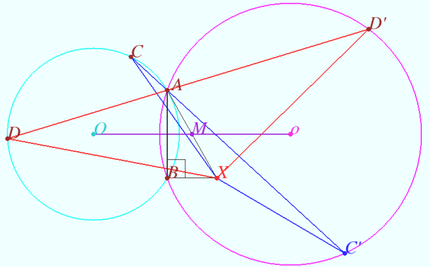
| + | Let <math>\triangle ACD \sim \triangle AC'D'.</math> | ||
| + | |||
| + | Let the points <math>O</math> and <math>O'</math> be the circumcenters of <math>\omega (\triangle ACD</math> and <math>\Omega (\triangle AC'D').</math> | ||
| + | |||
Let point <math>M</math> be the midpoint of <math>OO'.</math> | Let point <math>M</math> be the midpoint of <math>OO'.</math> | ||
| + | |||
The point <math>X</math> is symmetric to <math>A</math> with respect point <math>M.</math> | The point <math>X</math> is symmetric to <math>A</math> with respect point <math>M.</math> | ||
| + | |||
Prove that point <math>X</math> be the crosspoint of the bisectors <math>CC'</math> and <math>DD'.</math> | Prove that point <math>X</math> be the crosspoint of the bisectors <math>CC'</math> and <math>DD'.</math> | ||
<i><b>Proof</b></i> | <i><b>Proof</b></i> | ||
| − | <math>OM = MO', AM = MX \implies AOXO'</math> is parallelogram <math>\implies CO = AO = XO', C'O' = AO' = XO.</ | + | <math>OM = MO', AM = MX \implies AOXO'</math> is parallelogram <math>\implies</math> |
| − | Denote <math>\angle ADC = \angle AD'C' = alpha \implies \overset{\Large\frown} {AC} = \overset{\Large\frown} {AC'} = 2\alpha \implies \angle AOC = \angle AO'C' = 2 \alpha \implies \angle COX = 360^\circ - \angle AOX - 2 \alpha = \angle C'O'X \implies \triangle XOC = \triangle C'O'X \implies CX = C'X.</ | + | <cmath>CO = AO = XO', C'O' = AO' = XO.</cmath> |
| − | < | + | Denote <math>\angle ADC = \angle AD'C' = \alpha \implies \overset{\Large\frown} {AC} = \overset{\Large\frown} {AC'} = 2\alpha \implies</math> |
| + | |||
| + | <cmath>\angle AOC = \angle AO'C' = 2 \alpha \implies</cmath> | ||
| + | <cmath>\angle COX = 360^\circ - \angle AOX - 2 \alpha = \angle C'O'X \implies</cmath> | ||
| + | <cmath>\triangle XOC = \triangle C'O'X \implies CX = C'X.</cmath> | ||
| + | <cmath>\angle CXC' = \angle CXO + \angle OXO' + \angle O'XC'</cmath> | ||
| + | <cmath>\angle CXC' = \angle CXO + (180^\circ - \angle AOX) + \angle OCX</cmath> | ||
| + | <cmath>\angle CXC' = (180^\circ - \angle AOX) + (180^\circ - \angle COX).</cmath> | ||
| + | <cmath>\angle CXC' = 360^\circ - \angle AOX - \angle COX) = \angle AOC = 2 \alpha.</cmath> | ||
Similarly, <math>DX = D'X, \angle DXD' = 2 \angle ACD.</math> | Similarly, <math>DX = D'X, \angle DXD' = 2 \angle ACD.</math> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 15:45, 10 July 2023
Contents
- 1 Basic information
- 2 Simple problems
- 2.1 Explicit spiral symilarity
- 2.2 Hidden spiral symilarity
- 2.3 Linearity of the spiral symilarity
- 2.4 Construction of a similar triangle
- 2.5 Center of the spiral symilarity for similar triangles
- 2.6 Common point for 6 circles
- 2.7 Three spiral similarities
- 2.8 Superposition of two spiral similarities
- 2.9 Spiral similarity for circles
- 2.10 Remarkable point for spiral similarity
- 2.11 Remarkable point for pair of similar triangles
Basic information
A spiral similarity is a plane transformation composed of a rotation of the plane and a dilation of the plane having the common center. The order in which the composition is taken is not important.
Any two directly similar figures are related either by a translation or by a spiral similarity (directly similar figures are similar and have the same orientation).
The transformation is linear and transforms any given object into an object homothetic to given.
On the complex plane, any spiral similarity can be expressed in the form ![]() where
where ![]() is a complex number. The magnitude
is a complex number. The magnitude ![]() is the dilation factor of the spiral similarity, and the argument
is the dilation factor of the spiral similarity, and the argument ![]() is the angle of rotation.
is the angle of rotation.
The spiral similarity is uniquely defined by the images of two distinct points. It is easy to show using the complex plane.
Let ![]() with corresponding complex numbers
with corresponding complex numbers ![]() and
and ![]() so
so
![]()
![]()
![]() For any points
For any points ![]() and
and ![]() the center of the spiral similarity taking
the center of the spiral similarity taking ![]() to
to ![]() point
point ![]() is also the center of a spiral similarity taking
is also the center of a spiral similarity taking ![]() to
to ![]() This fact explain existance of Miquel point.
This fact explain existance of Miquel point.
Case 1 Any line segment ![]() can be mapped into any other
can be mapped into any other ![]() using the spiral similarity. Notation is shown on the diagram.
using the spiral similarity. Notation is shown on the diagram.
![]()
![]() is circle
is circle ![]() is circle
is circle ![]()
![]() is any point of
is any point of ![]() is circle
is circle ![]() is the image
is the image ![]() under spiral symilarity centered at
under spiral symilarity centered at ![]()
![]()
![]() is the dilation factor,
is the dilation factor,
![]() is the angle of rotation.
is the angle of rotation.
Case 2 Any line segment ![]() can be mapped into any other
can be mapped into any other ![]() using the spiral similarity. Notation is shown on the diagram.
using the spiral similarity. Notation is shown on the diagram. ![]() is circle
is circle ![]() (so circle is tangent to
(so circle is tangent to ![]() is circle tangent to
is circle tangent to ![]() is any point of
is any point of ![]() is circle
is circle ![]()
![]() is the image
is the image ![]() under spiral symilarity centered at
under spiral symilarity centered at ![]()
![]()
![]() is the dilation factor,
is the dilation factor,
![]() is the angle of rotation.
is the angle of rotation.
Simple problems
Explicit spiral symilarity
Given two similar right triangles ![]() and
and ![]()
![]() Find
Find ![]() and
and ![]()
Solution
The spiral symilarity centered at ![]() with coefficient
with coefficient ![]() and the angle of rotation
and the angle of rotation ![]() maps point
maps point ![]() to point
to point ![]() and point
and point ![]() to point
to point ![]()
Therefore this symilarity maps ![]() to
to ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Hidden spiral symilarity
Let ![]() be an isosceles right triangle
be an isosceles right triangle ![]() Let
Let ![]() be a point on a circle with diameter
be a point on a circle with diameter ![]() The line
The line ![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]() and intersects
and intersects ![]() at
at ![]() Prove that
Prove that ![]()
Proof
Denote ![]()
![]() Let
Let ![]() cross perpendicular to
cross perpendicular to ![]() in point
in point ![]() at point
at point ![]()
Then ![]()
Points ![]() and
and ![]() are simmetric with respect
are simmetric with respect ![]() so
so ![]()
The spiral symilarity centered at ![]() with coefficient
with coefficient ![]() and the angle of rotation
and the angle of rotation ![]() maps
maps ![]() to
to ![]() and
and ![]() to point
to point ![]() such that
such that ![]()
Therefore ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Linearity of the spiral symilarity
![]() Points
Points ![]() are outside
are outside ![]()
Prove that the centroids of triangles ![]() and
and ![]() are coinsite.
are coinsite.
Proof
Let ![]() where
where ![]() be the spiral similarity with the rotation angle
be the spiral similarity with the rotation angle ![]() and
and ![]()
A vector has two parameters, modulo and direction. It is not tied to a center of the spiral similarity. Therefore
![]()
![]() We use the property of linearity and get
We use the property of linearity and get
![]() Let
Let ![]() be the centroid of
be the centroid of ![]() so
so ![]()
![]() is the centroid of the
is the centroid of the ![]()
vladimir.shelomovskii@gmail.com, vvsss
Construction of a similar triangle
Let triangle ![]() and point
and point ![]() on sideline
on sideline ![]() be given. Construct
be given. Construct ![]() where
where ![]() lies on sideline
lies on sideline ![]() and
and ![]() lies on sideline
lies on sideline ![]()
Solution
Let ![]() be the spiral symilarity centered at
be the spiral symilarity centered at ![]() with the dilation factor
with the dilation factor ![]() and rotation angle
and rotation angle ![]()
![]() so image of any point
so image of any point ![]() lies on
lies on ![]()
![]() The spiral symilarity
The spiral symilarity ![]() centered at
centered at ![]() with the dilation factor
with the dilation factor ![]() and rotation angle
and rotation angle ![]() maps
maps ![]() into
into ![]() and
and ![]() therefore the found triangle
therefore the found triangle ![]() is the desired one.
is the desired one.
vladimir.shelomovskii@gmail.com, vvsss
Center of the spiral symilarity for similar triangles
Let triangle ![]() and point
and point ![]() on sideline
on sideline ![]() be given.
be given. ![]() where
where ![]() lies on sideline
lies on sideline ![]() and
and ![]() lies on sideline
lies on sideline ![]() The spiral symilarity
The spiral symilarity ![]() maps
maps ![]() into
into ![]() Prove
Prove
a) ![]()
b) Center of ![]() is the First Brocard point of triangles
is the First Brocard point of triangles ![]() and
and ![]()
Proof
a) Let ![]() be the spiral symilarity centered at
be the spiral symilarity centered at ![]() with the dilation factor
with the dilation factor ![]() and rotation angle
and rotation angle ![]()
![]()
Denote ![]()
![]() Similarly
Similarly ![]()
b) It is well known that the three circumcircles ![]() and
and ![]() have the common point (it is
have the common point (it is ![]() in the diagram).
in the diagram).
Therefore ![]() is cyclic and
is cyclic and ![]()
Similarly, ![]()
![]()
![]()
![]()
Similarly, ![]()
Therefore, ![]() is the First Brocard point of
is the First Brocard point of ![]()
![]() is cyclic
is cyclic ![]() Similarly,
Similarly, ![]()
Therefore ![]() is the First Brocard point of
is the First Brocard point of ![]() and
and ![]()
Therefore the spiral symilarity ![]() maps
maps ![]() into
into ![]() has the center
has the center ![]() the angle of the rotation
the angle of the rotation ![]()
vladimir.shelomovskii@gmail.com, vvsss
Common point for 6 circles
Let ![]() and point
and point ![]() on sideline
on sideline ![]() be given.
be given. ![]() where
where ![]() lies on sideline
lies on sideline ![]() and
and ![]() lies on sideline
lies on sideline ![]()
Denote ![]()
Prove that circumcircles of triangles ![]()
![]() have the common point.
have the common point.
Proof
![]() so there is the spiral symilarity
so there is the spiral symilarity ![]() taking
taking ![]() to
to ![]() Denote
Denote ![]() the center of
the center of ![]()
![]() the center of
the center of ![]() is the secont crosspoint of circumcircles of
is the secont crosspoint of circumcircles of ![]() and
and ![]() but this center is point
but this center is point ![]() so these circles contain point
so these circles contain point ![]() . Similarly for another circles.
. Similarly for another circles.
vladimir.shelomovskii@gmail.com, vvsss
Three spiral similarities
Let triangle ![]() be given. The triangle
be given. The triangle ![]() is constructed using a spiral similarity of
is constructed using a spiral similarity of ![]() with center
with center ![]() , angle of rotation
, angle of rotation ![]() and coefficient
and coefficient ![]()
A point ![]() is centrally symmetrical to a point
is centrally symmetrical to a point ![]() with respect to
with respect to ![]()
Prove that the spiral similarity with center ![]() , angle of rotation
, angle of rotation ![]() and coefficient
and coefficient ![]() taking
taking ![]() to
to ![]()
Proof
![]()
![]()
Corollary
Three spiral similarities centered on the images of the vertices of the given triangle ![]() and with rotation angles equal to the angles of
and with rotation angles equal to the angles of ![]() take
take ![]() to
to ![]() centrally symmetric to
centrally symmetric to ![]() with respect to
with respect to ![]()
vladimir.shelomovskii@gmail.com, vvsss
Superposition of two spiral similarities
Let ![]() be the spiral similarity centered at
be the spiral similarity centered at ![]() with angle
with angle ![]() and coefficient
and coefficient ![]()
Let ![]() be spiral similarity centered at
be spiral similarity centered at ![]() with angle
with angle ![]() and coefficient
and coefficient ![]()
Let ![]()
Prove:
a) ![]() is the crosspoint of bisectors
is the crosspoint of bisectors ![]() and
and ![]()
b)![]()
Algebraic proof
We use the complex plane ![]()
![]()
![]() Let
Let ![]() Then
Then ![]() Geometric proof
Geometric proof
Denote ![]()
Then ![]()
Let ![]() be the midpoint
be the midpoint ![]() be the point on bisector
be the point on bisector ![]() such that
such that ![]() be the point on bisector
be the point on bisector ![]() such that
such that ![]() Then
Then
![]()
![]()
![]()
![]()
![]()
![]() is the crosspoint of bisectors
is the crosspoint of bisectors ![]() and
and ![]()
Corollary
There is another pare of the spiral similarities centered at ![]() and
and ![]() with angle
with angle ![]() coefficients
coefficients ![]() and
and ![]()
In this case ![]()
vladimir.shelomovskii@gmail.com, vvsss
Spiral similarity for circles
1. Let circle ![]() cross circle
cross circle ![]() at points
at points ![]() and
and ![]() Point
Point ![]() lies on
lies on ![]()
Spiral similarity ![]() centered at
centered at ![]() maps
maps ![]() into
into ![]()
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
Arcs ![]()
![]()
![]()
Corollary
Let ![]() points
points ![]() and
and ![]() be collinear.
be collinear.
Then exist the spiral similarity ![]() centered at
centered at ![]() such that
such that ![]()
2. Let circle ![]() cross circle
cross circle ![]() at points
at points ![]() and
and ![]()
Points ![]() and
and ![]() lie on
lie on ![]()
Let ![]() be the tangent to
be the tangent to ![]() be the tangent to
be the tangent to ![]()
Prove that angle between tangents is equal angle between lines ![]() and
and ![]()
Proof
There is the spiral similarity ![]() centered at
centered at ![]() such that
such that ![]() Therefore
Therefore ![]() angles between these lines are the same.
angles between these lines are the same.
vladimir.shelomovskii@gmail.com, vvsss
Remarkable point for spiral similarity
Circles ![]() and
and ![]() centered at points
centered at points ![]() and
and ![]() respectively intersect at points
respectively intersect at points ![]() and
and ![]() Points
Points ![]() and
and ![]() are collinear. Point
are collinear. Point ![]() is symmetrical to
is symmetrical to ![]() with respect to the midpoint
with respect to the midpoint ![]() point
point ![]() Prove:
Prove:
a) ![]() b)
b) ![]()
Proof
a) ![]() cross
cross ![]() in midpoint
in midpoint ![]()
b) ![]() is parallelogram
is parallelogram ![]()
Denote ![]()
![]()
![]()
![]()
![]()
![]()
Corollary
Let points ![]() and
and ![]() be collinear. Then
be collinear. Then ![]()
Therefore ![]() is the crosspoint of the bisectors
is the crosspoint of the bisectors ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
Remarkable point for pair of similar triangles
Let ![]()
Let the points ![]() and
and ![]() be the circumcenters of
be the circumcenters of ![]() and
and ![]()
Let point ![]() be the midpoint of
be the midpoint of ![]()
The point ![]() is symmetric to
is symmetric to ![]() with respect point
with respect point ![]()
Prove that point ![]() be the crosspoint of the bisectors
be the crosspoint of the bisectors ![]() and
and ![]()
Proof
![]() is parallelogram
is parallelogram ![]()
![]() Denote
Denote ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Similarly,
Similarly, ![]()
vladimir.shelomovskii@gmail.com, vvsss