Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Spiral similarity"
(→‎Hidden spiral symilarity)
Line 24: Line 24:
 
<math>\arg(k) =\angle APA'=\angle Ax_0A' =\angle Bx_0B' =\angle Cx_0C'</math> is the angle of rotation.
 
<math>\arg(k) =\angle APA'=\angle Ax_0A' =\angle Bx_0B' =\angle Cx_0C'</math> is the angle of rotation.
 
==Hidden  spiral symilarity==
 
==Hidden  spiral symilarity==
 +
[[File:1932a Pras.png|450px|right]]
 
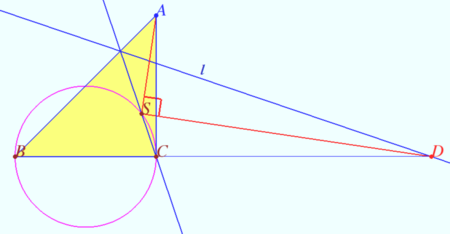
Let <math>\triangle ABC</math> be an isosceles right triangle <math>(AC = BC).</math> Let <math>S</math> be a point on a circle with diameter <math>BC.</math> The line <math>\ell</math> is symmetrical to <math>SC</math> with respect to <math>AB</math> and intersects <math>BC</math> at <math>D.</math> Prove that <math>AS \perp DS.</math>
 
Let <math>\triangle ABC</math> be an isosceles right triangle <math>(AC = BC).</math> Let <math>S</math> be a point on a circle with diameter <math>BC.</math> The line <math>\ell</math> is symmetrical to <math>SC</math> with respect to <math>AB</math> and intersects <math>BC</math> at <math>D.</math> Prove that <math>AS \perp DS.</math>
  
 
<i><b>Proof</b></i>
 
<i><b>Proof</b></i>
 +
 +
Denote <math>\angle SBC = \alpha, \angle SCB = \beta = 90^\circ - \alpha,</math>
 +
<cmath>\angle SCA = \alpha, \angle BSC = 90^\circ, k = \frac {SC}{SB} = \cot \beta.</cmath>
 +
Let <math>SC</math> cross perpendicular to <math>BC</math> in point <math>B</math> at point <math>D'.</math>
 +
 +
Then <math>\frac {BC}{BD'} = \cot \beta.</math>
 +
 +
Points <math>D</math> and <math>D'</math> are simmetric with respect <math>AB,</math> so <math>BD = BD' \implies k = \frac {SC}{SB} = \frac {BC}{BD}.</math>
 +
 +
The spiral symilarity centered at <math>S</math> with coefficient <math>k</math> and the angle of rotation <math>90^\circ</math> maps <math>B</math> to <math>C</math> and <math>D</math> to point <math>D_0</math> such that <math>k \cdot BD_0 = BC = AC, \angle D_0CS = \angle DBS \implies D_0 = A.</math>
 +
Therefore <math>\angle ASC = \angle DSB \implies \angle ASD = \angle ASC - \angle DSC = \angle DSB - \angle DSC = \angle BSC = - \angle DSC = 90^\circ.</math>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 14:22, 10 June 2023

A spiral similarity is a plane transformation composed of a rotation of the plane and a dilation of the plane having the common center. The order in which the composition is taken is not important.

The transformation is linear and transforms any given object into an object homothetic to given.

On the complex plane, any spiral similarity can be expressed in the form $T(x) = x_0+k (x-x_0),$ where $k$ is a complex number. The magnitude $|k|$ is the dilation factor of the spiral similarity, and the argument $\arg(k)$ is the angle of rotation.

The spiral similarity is uniquely defined by the images of two distinct points. It is easy to show using the complex plane.

Spiral center.png

Let $A' = T(A), B' = T(B),$ with corresponding complex numbers $a', a, b',$ and $b,$ so \[a' = T(a) = x_0 + k (a - x_0), b' = T(b) = x_0+ k (b-x_0) \implies\] \[k = \frac {T(b) - T(a)}{b-a} = \frac {b' - a' }{b - a},\] \[x_0=\frac {ab' - ba' }{a-a'+b' -b}, a' - a \ne b' - b.\]

Any line segment $AB$ can be mapped into any other $A'B'$ using the spiral similarity. Notation is shown on the diagram. $P = AB \cap A'B'.$

$\Omega$ is circle $AA'P, \omega$ is circle $BB'P, x_0 = \Omega \cap \omega, x_0 \neq P,$

$C$ is any point of $AB, \theta$ is circle $CPx_0, C' = \theta \cap A'B'$ is the image $C$ under spiral symilarity centered at $x_0.$

$|k| = \frac {A'B'}{AB} = \frac {A'x_0}{Ax_0} = \frac {B'x_0}{Bx_0} = \frac {C'x_0}{Cx_0}$ is the dilation factor,

$\arg(k) =\angle APA'=\angle Ax_0A' =\angle Bx_0B' =\angle Cx_0C'$ is the angle of rotation.

Hidden spiral symilarity

1932a Pras.png

Let $\triangle ABC$ be an isosceles right triangle $(AC = BC).$ Let $S$ be a point on a circle with diameter $BC.$ The line $\ell$ is symmetrical to $SC$ with respect to $AB$ and intersects $BC$ at $D.$ Prove that $AS \perp DS.$

Proof

Denote $\angle SBC = \alpha, \angle SCB = \beta = 90^\circ - \alpha,$ \[\angle SCA = \alpha, \angle BSC = 90^\circ, k = \frac {SC}{SB} = \cot \beta.\] Let $SC$ cross perpendicular to $BC$ in point $B$ at point $D'.$

Then $\frac {BC}{BD'} = \cot \beta.$

Points $D$ and $D'$ are simmetric with respect $AB,$ so $BD = BD' \implies k = \frac {SC}{SB} = \frac {BC}{BD}.$

The spiral symilarity centered at $S$ with coefficient $k$ and the angle of rotation $90^\circ$ maps $B$ to $C$ and $D$ to point $D_0$ such that $k \cdot BD_0 = BC = AC, \angle D_0CS = \angle DBS \implies D_0 = A.$ Therefore $\angle ASC = \angle DSB \implies \angle ASD = \angle ASC - \angle DSC = \angle DSB - \angle DSC = \angle BSC = - \angle DSC = 90^\circ.$ vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Spiral_similarity&oldid=194149"