Difference between revisions of "1989 AIME Problems/Problem 12"
(→See also) |
|||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
| − | {{ | + | Call the midpoint of AB M and the midpoint of CD N. d is the median of triangle <math>\triangle CDM</math>. The formula for the length of a median is <math>m=\sqrt{\frac{2a^2+2b^2-c^2}{4}}</math>, where a, b, and c are the side lengths of triangle, and c is the side that is bisected by median m. |
| + | |||
| + | We first find CM, which is the median of <math>\triangle CAB</math>. | ||
| + | |||
| + | <math>CM=\sqrt{\frac{98+2592-1681}{4}}=\frac{\sqrt{1009}}{2}</math> | ||
| + | |||
| + | Now we must find DM, which is the median of <math>\triangle DAB</math>. | ||
| + | |||
| + | <math>DM=\frac{\sqrt{425}}{2}</math> | ||
| + | |||
| + | Now that we know the sides of <math>\triangle CDM</math>, we proceed to find the length of d. | ||
| + | |||
| + | <math>d=\frac{\sqrt{548}}{2}</math> | ||
| + | |||
| + | <math>d^2=\frac{548}{4}=\boxed{137}</math> | ||
| + | |||
== See also == | == See also == | ||
{{AIME box|year=1989|num-b=11|num-a=13}} | {{AIME box|year=1989|num-b=11|num-a=13}} | ||
Revision as of 07:47, 12 November 2007
Problem
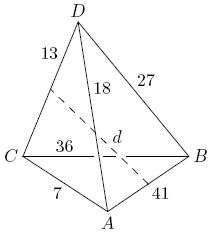
Let ![]() be a tetrahedron with
be a tetrahedron with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , as shown in the figure. Let
, as shown in the figure. Let ![]() be the distance between the midpoints of edges
be the distance between the midpoints of edges ![]() and
and ![]() . Find
. Find ![]() .
.
Solution
Call the midpoint of AB M and the midpoint of CD N. d is the median of triangle ![]() . The formula for the length of a median is
. The formula for the length of a median is ![]() , where a, b, and c are the side lengths of triangle, and c is the side that is bisected by median m.
, where a, b, and c are the side lengths of triangle, and c is the side that is bisected by median m.
We first find CM, which is the median of ![]() .
.
![]()
Now we must find DM, which is the median of ![]() .
.
![]()
Now that we know the sides of ![]() , we proceed to find the length of d.
, we proceed to find the length of d.
![]()
![]()
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||