Difference between revisions of "2002 AMC 12A Problems/Problem 25"
(→Solution) |
m (→Solution) |
||
| Line 5: | Line 5: | ||
[[File:2002AMC12A25.png]] | [[File:2002AMC12A25.png]] | ||
| − | ==Solution== | + | ==Solution 1== |
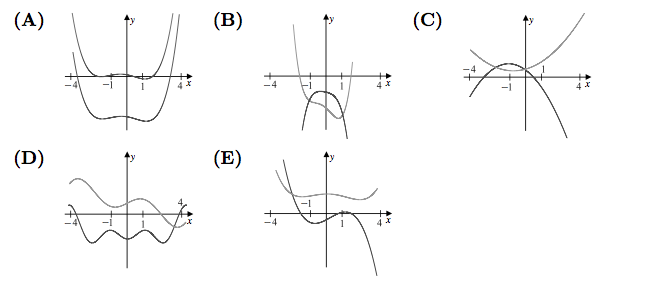
The sum of the coefficients of <math>P</math> and of <math>Q</math> will be equal, so <math>P(1) = Q(1)</math>. The only answer choice with an intersection between the two graphs at <math>x = 1</math> is '''(B)'''. (The polynomials in the graph are <math>P(x) = 2x^4-3x^2-3x-4</math> and <math>Q(x) = -2x^4-2x^2-2x-2</math>.) | The sum of the coefficients of <math>P</math> and of <math>Q</math> will be equal, so <math>P(1) = Q(1)</math>. The only answer choice with an intersection between the two graphs at <math>x = 1</math> is '''(B)'''. (The polynomials in the graph are <math>P(x) = 2x^4-3x^2-3x-4</math> and <math>Q(x) = -2x^4-2x^2-2x-2</math>.) | ||
Revision as of 00:25, 11 April 2023
Contents
Problem
The nonzero coefficients of a polynomial 
with real coefficients are all replaced by their mean to form a polynomial 
. Which of the following could be a graph of 
and 
over the interval 
?
Solution 1
The sum of the coefficients of and of will be equal, so 
. The only answer choice with an intersection between the two graphs at 
is (B). (The polynomials in the graph are 
and 
.)
Solution 2
We know every coefficient is equal, so we get 
which equals 
. We see apparently that x cannot be positive, for it would yield a number greater than zero for 
. We look at the zeros of the answer choices. A, C, D, and E have a positive zero, which eliminates them. B is the answer.
See Also
| 2002 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
