Difference between revisions of "Isogonal conjugate"
(→The isogonal theorem) |
(→The isogonal theorem) |
||
| Line 41: | Line 41: | ||
Preimages of the points <math>Z</math> and <math>Z'</math> lie on the isogonals. | Preimages of the points <math>Z</math> and <math>Z'</math> lie on the isogonals. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
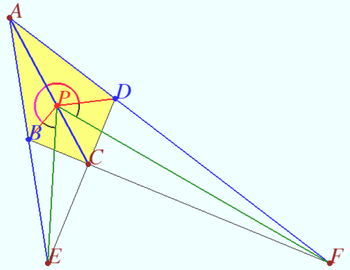
| + | ==Isogonal of the diagonal of a quadrilateral== | ||
| + | [[File:Quadrungle isogonals.png|350px|right]] | ||
| + | Given a quadrilateral <math>ABCD</math> and a point <math>P</math> on its diagonal such that <math>\angle APB = \angle APD.</math> Let <math>E = AB \cap CD, F = AD \cap BC.</math> Prove that <math>\angle EPB = \angle FPD.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let us perform a projective transformation of the plane that maps the point <math>P</math> to a point at infinity and the line <math>\ell = AC</math> into itself. In this case, the images of points <math>B</math> and <math>D</math> are equidistant from the image of <math>AC \implies</math> | ||
| + | |||
| + | the point <math>M</math> (midpoint of BD) lies on <math>L \implies AC</math> contains the midpoints of <math>AC</math> and <math>BD,</math> that is, <math>\ell</math> is the Gauss line of the complete quadrilateral <math>ABCDEF \implies \ell</math> bisects <math>EF \implies EE_0 = FF_0 \implies</math> the preimages of the points <math>E</math> and <math>F</math> lie on the isogonals <math>PE</math> and <math>PF.</math> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 15:32, 26 February 2023
Isogonal conjugates are pairs of points in the plane with respect to a certain triangle.
Contents
- 1 The isogonal theorem
- 2 Isogonal of the diagonal of a quadrilateral
- 3 Definition of isogonal conjugate of a point
- 4 Second definition
- 5 Distance to the sides of the triangle
- 6 Sign of isogonally conjugate points
- 7 Circumcircle of pedal triangles
- 8 Common circumcircle of the pedal triangles as the sign of isogonally conjugate points
- 9 Circles
- 10 Problems
The isogonal theorem
Isogonal lines definition
Let a line ![]() and a point
and a point ![]() lying on
lying on ![]() be given. A pair of lines symmetric with respect to
be given. A pair of lines symmetric with respect to ![]() and containing the point
and containing the point ![]() be called isogonals with respect to the pair
be called isogonals with respect to the pair ![]()
Sometimes it is convenient to take one pair of isogonals as the base one, for example, ![]() and
and ![]() are the base pair. Then we call the remaining pairs as isogonals with respect to the angle
are the base pair. Then we call the remaining pairs as isogonals with respect to the angle ![]()
Projective transformation
It is known that the transformation that maps a point with coordinates ![]() into a point with coordinates
into a point with coordinates ![]() is projective.
is projective.
If the abscissa axis coincides with the line ![]() and the origin coincides with the point
and the origin coincides with the point ![]() then the isogonals define the equations
then the isogonals define the equations ![]() and the lines
and the lines ![]() symmetrical with respect to the line
symmetrical with respect to the line ![]() become their images.
become their images.
It is clear that, under the reverse transformation (also projective), such pairs of lines become isogonals, and the points equidistant from ![]() lie on the isogonals.
lie on the isogonals.
The isogonal theorem
Let two pairs of isogonals ![]() and
and ![]() be given. Let lines
be given. Let lines ![]() and
and ![]() intersect at point
intersect at point ![]() Let lines
Let lines ![]() and
and ![]() intersect at point
intersect at point ![]() Prove that
Prove that ![]() and
and ![]() are the isogonals with respect to the pair
are the isogonals with respect to the pair ![]()
Proof
Let us perform a projective transformation of the plane that maps the point ![]() into a point at infinity and the line
into a point at infinity and the line ![]() maps to itself. In this case, the isogonals turn into a pair of straight lines parallel to
maps to itself. In this case, the isogonals turn into a pair of straight lines parallel to ![]() and equidistant from
and equidistant from ![]()
The reverse (also projective) transformation maps the points equidistant from ![]() onto isogonals.
onto isogonals.
Let the images of isogonals are vertical lines. Let coordinates of images of points be ![]() Equation of a straight line
Equation of a straight line ![]() is
is ![]()
Equation of a straight line ![]() is
is ![]()
Point ![]() abscissa
abscissa ![]()
Equation of a straight line ![]() is
is ![]()
Equation of a straight line ![]() is
is ![]()
Point ![]() abscissa
abscissa ![]()
Preimages of the points ![]() and
and ![]() lie on the isogonals.
lie on the isogonals.
vladimir.shelomovskii@gmail.com, vvsss
Isogonal of the diagonal of a quadrilateral
Given a quadrilateral ![]() and a point
and a point ![]() on its diagonal such that
on its diagonal such that ![]() Let
Let ![]() Prove that
Prove that ![]()
Proof
Let us perform a projective transformation of the plane that maps the point ![]() to a point at infinity and the line
to a point at infinity and the line ![]() into itself. In this case, the images of points
into itself. In this case, the images of points ![]() and
and ![]() are equidistant from the image of
are equidistant from the image of ![]()
the point ![]() (midpoint of BD) lies on
(midpoint of BD) lies on ![]() contains the midpoints of
contains the midpoints of ![]() and
and ![]() that is,
that is, ![]() is the Gauss line of the complete quadrilateral
is the Gauss line of the complete quadrilateral ![]() bisects
bisects ![]() the preimages of the points
the preimages of the points ![]() and
and ![]() lie on the isogonals
lie on the isogonals ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
Definition of isogonal conjugate of a point
Let ![]() be a point in the plane, and let
be a point in the plane, and let ![]() be a triangle. We will denote by
be a triangle. We will denote by ![]() the lines
the lines ![]() . Let
. Let ![]() denote the lines
denote the lines ![]() ,
, ![]() ,
, ![]() , respectively. Let
, respectively. Let ![]() ,
, ![]() ,
, ![]() be the reflections of
be the reflections of ![]() ,
, ![]() ,
, ![]() over the angle bisectors of angles
over the angle bisectors of angles ![]() ,
, ![]() ,
, ![]() , respectively. Then lines
, respectively. Then lines ![]() ,
, ![]() ,
, ![]() concur at a point
concur at a point ![]() , called the isogonal conjugate of
, called the isogonal conjugate of ![]() with respect to triangle
with respect to triangle ![]() .
.
Proof
By our constructions of the lines ![]() ,
, ![]() , and this statement remains true after permuting
, and this statement remains true after permuting ![]() . Therefore by the trigonometric form of Ceva's Theorem
. Therefore by the trigonometric form of Ceva's Theorem
![]() so again by the trigonometric form of Ceva, the lines
so again by the trigonometric form of Ceva, the lines ![]() concur, as was to be proven.
concur, as was to be proven. ![]()
Second definition
Let triangle ![]() be given. Let point
be given. Let point ![]() lies in the plane of
lies in the plane of ![]()
![]() Let the reflections of
Let the reflections of ![]() in the sidelines
in the sidelines ![]() be
be ![]()
Then the circumcenter ![]() of the
of the ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]()
Points ![]() and
and ![]() have not isogonal conjugate points.
have not isogonal conjugate points.
Another points of sidelines ![]() have points
have points ![]() respectively as isogonal conjugate points.
respectively as isogonal conjugate points.
Proof
![]()
![]()
![]()
![]() common
common ![]()
![]() Similarly
Similarly ![]() is the circumcenter of the
is the circumcenter of the ![]()
![]()
From definition 1 we get that ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]()
It is clear that each point ![]() has the unique isogonal conjugate point.
has the unique isogonal conjugate point.
Let point ![]() be the point with barycentric coordinates
be the point with barycentric coordinates ![]()
![]() Then
Then ![]() has barycentric coordinates
has barycentric coordinates ![]()
vladimir.shelomovskii@gmail.com, vvsss
Distance to the sides of the triangle
Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Let ![]() and
and ![]() be the projection
be the projection ![]() on sides
on sides ![]() and
and ![]() respectively.
respectively.
Let ![]() and
and ![]() be the projection
be the projection ![]() on sides
on sides ![]() and
and ![]() respectively.
respectively.
Then ![]()
Proof
Let ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Sign of isogonally conjugate points
Let triangle ![]() and points
and points ![]() and
and ![]() inside it be given.
inside it be given.
Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
respectively.
Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
respectively.
Let ![]() Prove that point
Prove that point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
One can prove similar theorem in the case ![]() outside
outside ![]()
Proof
![]()
![]()
Denote ![]()
![]()
![]()
![]()
![]()
![]() Similarly
Similarly ![]() point
point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
vladimir.shelomovskii@gmail.com, vvsss
Circumcircle of pedal triangles
Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() Let
Let ![]() be the projection
be the projection ![]() on sides
on sides ![]() respectively.
respectively.
Let ![]() be the projection
be the projection ![]() on sides
on sides ![]() respectively.
respectively.
Then points ![]() are concyclic.
are concyclic.
The midpoint ![]() is circumcenter of
is circumcenter of ![]()
Proof
Let ![]()
![]() Hence points
Hence points ![]() are concyclic.
are concyclic.
![]() is trapezoid,
is trapezoid, ![]()
the midpoint ![]() is circumcenter of
is circumcenter of ![]()
Similarly points ![]() are concyclic and points
are concyclic and points ![]() are concyclic.
are concyclic.
Therefore points ![]() are concyclic, so the midpoint
are concyclic, so the midpoint ![]() is circumcenter of
is circumcenter of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Common circumcircle of the pedal triangles as the sign of isogonally conjugate points
Let triangle ![]() and points
and points ![]() and
and ![]() inside it be given. Let
inside it be given. Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
Let
respectively.
Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
respectively.
Let points ![]() be concyclic and none of them lies on the sidelines of
be concyclic and none of them lies on the sidelines of ![]()
Then point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
This follows from the uniqueness of the conjugate point and the fact that the line intersects the circle in at most two points.
vladimir.shelomovskii@gmail.com, vvsss
Circles
Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() Let
Let ![]() be the circumcenter of
be the circumcenter of ![]() Let
Let ![]() be the circumcenter of
be the circumcenter of ![]() Prove that points
Prove that points ![]() and
and ![]() are inverses with respect to the circumcircle of
are inverses with respect to the circumcircle of ![]()
Proof
The circumcenter of ![]() point
point ![]() and points
and points ![]() and
and ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]()
![]()
![]()
![]() Similarly
Similarly ![]()
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Problems
Olympiad
Given a nonisosceles, nonright triangle ![]() let
let ![]() denote the center of its circumscribed circle, and let
denote the center of its circumscribed circle, and let ![]() and
and ![]() be the midpoints of sides
be the midpoints of sides ![]() and
and ![]() respectively. Point
respectively. Point ![]() is located on the ray
is located on the ray ![]() so that
so that ![]() is similar to
is similar to ![]() . Points
. Points ![]() and
and ![]() on rays
on rays ![]() and
and ![]() respectively, are defined similarly. Prove that lines
respectively, are defined similarly. Prove that lines ![]() and
and ![]() are concurrent, i.e. these three lines intersect at a point. (Source)
are concurrent, i.e. these three lines intersect at a point. (Source)
Let ![]() be a given point inside quadrilateral
be a given point inside quadrilateral ![]() . Points
. Points ![]() and
and ![]() are located within
are located within ![]() such that
such that ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Prove that
. Prove that ![]() if and only if
if and only if ![]() . (Source)
. (Source)