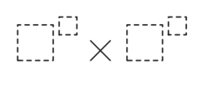Difference between revisions of "2023 AMC 8 Problems/Problem 6"
Grapecoder (talk | contribs) |
|||
| Line 1: | Line 1: | ||
| + | ==Problem== | ||
| + | The digits 2, 0, 2, and 3 are placed in the expression below, one digit per box. What is the maximum | ||
| + | possible value of the expression? | ||
| + | [[File:2023 AMC 8-6.png|200px|thumb|center]] | ||
| + | |||
| + | <math>\textbf{(A) }0 \qquad \textbf{(B) }8 \qquad \textbf{(C) }9 \qquad \textbf{(D) }16 \qquad \textbf{(E) }18</math> | ||
| + | |||
==Solution 1== | ==Solution 1== | ||
First, let us consider the cases where <math>0</math> is a base. This would result in the entire expression being <math>0</math>. However, if <math>0</math> is an exponent, we will get a value greater than <math>0</math>. As <math>3^2\cdot2^0=9</math> is greater than <math>2^3\cdot2^0=8</math> and <math>2^2\cdot3^0=4</math>, the answer is <math>\boxed{\textbf{(C) }9}</math>. | First, let us consider the cases where <math>0</math> is a base. This would result in the entire expression being <math>0</math>. However, if <math>0</math> is an exponent, we will get a value greater than <math>0</math>. As <math>3^2\cdot2^0=9</math> is greater than <math>2^3\cdot2^0=8</math> and <math>2^2\cdot3^0=4</math>, the answer is <math>\boxed{\textbf{(C) }9}</math>. | ||
Revision as of 00:24, 25 January 2023
Problem
The digits 2, 0, 2, and 3 are placed in the expression below, one digit per box. What is the maximum possible value of the expression?
![]()
Solution 1
First, let us consider the cases where ![]() is a base. This would result in the entire expression being
is a base. This would result in the entire expression being ![]() . However, if
. However, if ![]() is an exponent, we will get a value greater than
is an exponent, we will get a value greater than ![]() . As
. As ![]() is greater than
is greater than ![]() and
and ![]() , the answer is
, the answer is ![]() .
.
~MathFun1000
Solution 2
The maximum possible value of using the digit ![]() . We can maximize our value by keeping the
. We can maximize our value by keeping the ![]() and
and ![]() together in one power. (Biggest with biggest and smallest with smallest) This shows
together in one power. (Biggest with biggest and smallest with smallest) This shows ![]() =
=![]() =
=![]() . (Don't want
. (Don't want ![]() cause that's
cause that's ![]() ) It is going to be
) It is going to be ![]()
~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing))