Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Gossard perspector"

(→‎Gossard perspector and Gossard triangle for equilateral triangle)
(→‎Gossard perspector and Gossard triangle for equilateral triangle)
Line 30: Line 30:
 
It is clear that the Euler line of equilateral <math>\triangle ABC (AB = AC)</math> meet the sidelines <math>BC, CA</math> and <math>AB</math> of <math>\triangle ABC</math> at <math>A'</math> and <math>A,</math> where <math>A'</math> is the midpoint of <math>BC.</math>
 
It is clear that the Euler line of equilateral <math>\triangle ABC (AB = AC)</math> meet the sidelines <math>BC, CA</math> and <math>AB</math> of <math>\triangle ABC</math> at <math>A'</math> and <math>A,</math> where <math>A'</math> is the midpoint of <math>BC.</math>
  
−
Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines of the <math>\triangle AA'B, \triangle AA'C,</math> and the line <math>l</math> contains <math>A</math> and parallel to <math>BC,</math> the vertex <math>B'</math> being the intersection of the Euler line of the <math>\triangle AA'C</math> and <math>l,</math> the vertex <math>C'</math> being the intersection of the Euler line of the <math>\triangle AA'B</math> and <math>l.</math> We call the triangle <math>\triangle A'B'C'</math> as the Gossard triangle of <math>\triangle ABC.</math>
+
Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines of the <math>\triangle AA'B, \triangle AA'C,</math> and the line <math>l</math> contains <math>A</math> and parallel to <math>BC,</math> the vertex <math>B'</math> being the intersection of the Euler line of the <math>\triangle AA'C</math> and <math>l,</math> the vertex <math>C'</math> being the intersection of the Euler line of the <math>\triangle AA'B</math> and <math>l.</math>
 +
 
 +
We call the triangle <math>\triangle A'B'C'</math> as the Gossard triangle of <math>\triangle ABC.</math>
  
 
Let <math>\triangle ABC</math> be any equilateral triangle and let  <math>\triangle A'B'C'</math> be its Gossard triangle. Then the lines <math>AA', BB',</math> and <math>CC'</math> are concurrent. We call the point of concurrence <math>Go</math> as  the Gossard perspector of <math>\triangle ABC.</math>  Let <math>H</math> be the orthocenter of <math>\triangle ABC, O</math> be the circumcenter of <math>\triangle ABC.</math>
 
Let <math>\triangle ABC</math> be any equilateral triangle and let  <math>\triangle A'B'C'</math> be its Gossard triangle. Then the lines <math>AA', BB',</math> and <math>CC'</math> are concurrent. We call the point of concurrence <math>Go</math> as  the Gossard perspector of <math>\triangle ABC.</math>  Let <math>H</math> be the orthocenter of <math>\triangle ABC, O</math> be the circumcenter of <math>\triangle ABC.</math>
  
 
It is clear that <math>Go</math> is the midpoint of <math>AA'.</math>
 
It is clear that <math>Go</math> is the midpoint of <math>AA'.</math>
−
<math>M = A'C' \cap AB</math> is the midpoint <math>AB, N = A'B' \cap AC</math> is the midpoint <math>AC, \triangle A'BM = \triangle CNA' \sim \triangle CBA</math> with coefficient <math>k = \frac {1}{2}.</math>
+
<math>M = A'C' \cap AB</math> is the midpoint <math>AB, N = A'B' \cap AC</math> is the midpoint <math>AC.</math>
 +
 
 +
<math>\triangle A'BM = \triangle CNA' \sim \triangle CBA</math> with coefficient <math>k = \frac {1}{2}.</math>
  
 
Any equilateral  triangle and its Gossard triangle are congruent.
 
Any equilateral  triangle and its Gossard triangle are congruent.
 +
 
Any equilateral  triangle and its Gossard triangle have the same Euler line.
 
Any equilateral  triangle and its Gossard triangle have the same Euler line.
 +
 
The Gossard triangle of the equilateral  <math>\triangle ABC</math> is the reflection of <math>\triangle ABC</math> in the Gossard perspector.
 
The Gossard triangle of the equilateral  <math>\triangle ABC</math> is the reflection of <math>\triangle ABC</math> in the Gossard perspector.
 
Denote <math>\angle BAC = \alpha, \angle ABC = \angle ACB = \beta, AO = BO = R \implies</math>
 
Denote <math>\angle BAC = \alpha, \angle ABC = \angle ACB = \beta, AO = BO = R \implies</math>
−
<math>\sin \beta = \cos \frac {\alpha}{2}, GoO = AO – AGo = R \cdot \frac{1 – \cos  {\alpha}}{2},</math>
+
<cmath>\sin \beta = \cos \frac {\alpha}{2}, GoO = AO – AGo = R \cdot \frac{1 – \cos  {\alpha}}{2},</cmath>
−
$OH = AH – AO = R(2 \cos \alpha – 1)  \implies \vec {GoO} = \vec {OH} \cdot \frac {1 – \cos \alpha}{2(2 \cos \alpha – 1)}.
+
<cmath>OH = AH – AO = R(2 \cos \alpha – 1)  \implies \vec {GoO} = \vec {OH} \cdot \frac {1 – \cos \alpha}{2(2 \cos \alpha – 1)}.</cmath>
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 12:24, 10 January 2023

Gossard perspector X(402) and Gossard triangle

Euler proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is parallel with the third side of the given triangle.

Gossard proved that the three Euler lines of the triangles formed by the Euler line and the sides, taken by twos, of a given triangle, form a triangle triply perspective with the given triangle and having the same Euler line. The orthocenters, circumcenters and centroids of these two triangles are symmetrically placed as to the center of perspective which known as Gossard perspector or Kimberling point $X(402).$

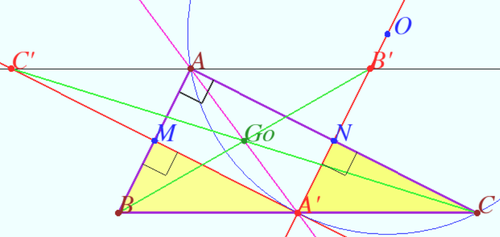
Gossard perspector of right triangle

Gossard 90.png

It is clear that the Euler line of right triangle $ABC (\angle A = 90 ^\circ)$ meet the sidelines $BC, CA$ and $AB$ of $\triangle ABC$ at $A'$ and $A,$ where $A'$ is the midpoint of $BC.$

Let $\triangle A'B'C'$ be the triangle formed by the Euler lines of the $\triangle AA'B, \triangle AA'C,$ and the line $l$ contains $A$ and parallel to $BC,$ the vertex $B'$ being the intersection of the Euler line of the $\triangle AA'C$ and $l,$ the vertex $C'$ being the intersection of the Euler line of the $\triangle AA'B$ and $l.$

We call the triangle $\triangle A'B'C'$ as the Gossard triangle of $\triangle ABC.$

Let $\triangle ABC$ be any right triangle and let $\triangle A'B'C'$ be its Gossard triangle. Then the lines $AA', BB',$ and $CC'$ are concurrent. We call the point of concurrence $Go$ as the Gossard perspector of $\triangle ABC.$

$Go$ is the midpoint of $AA'.$ $A$ is orthocenter of $\triangle ABC, A'$ is circumcenter of $\triangle ABC,$ so $Go$ is midpoint of $OH.$

$M = A'C' \cap AB$ is the midpoint $AB, N = A'B' \cap AC$ is the midpoint $AC, \triangle A'BM = \triangle CNA' \sim \triangle CBA$ with coefficient $k = \frac {1}{2}.$

Any right triangle and its Gossard triangle are congruent.

Any right triangle and its Gossard triangle have the same Euler line.

The Gossard triangle of the right $\triangle ABC$ is the reflection of $\triangle ABC$ in the Gossard perspector.

vladimir.shelomovskii@gmail.com, vvsss

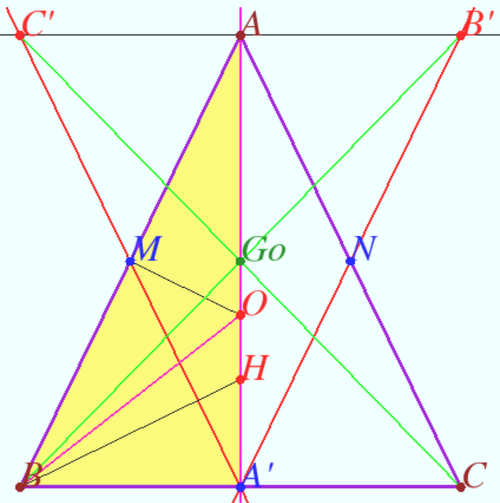
Gossard perspector and Gossard triangle for equilateral triangle

Gossard equilateral.png

It is clear that the Euler line of equilateral $\triangle ABC (AB = AC)$ meet the sidelines $BC, CA$ and $AB$ of $\triangle ABC$ at $A'$ and $A,$ where $A'$ is the midpoint of $BC.$

Let $\triangle A'B'C'$ be the triangle formed by the Euler lines of the $\triangle AA'B, \triangle AA'C,$ and the line $l$ contains $A$ and parallel to $BC,$ the vertex $B'$ being the intersection of the Euler line of the $\triangle AA'C$ and $l,$ the vertex $C'$ being the intersection of the Euler line of the $\triangle AA'B$ and $l.$

We call the triangle $\triangle A'B'C'$ as the Gossard triangle of $\triangle ABC.$

Let $\triangle ABC$ be any equilateral triangle and let $\triangle A'B'C'$ be its Gossard triangle. Then the lines $AA', BB',$ and $CC'$ are concurrent. We call the point of concurrence $Go$ as the Gossard perspector of $\triangle ABC.$ Let $H$ be the orthocenter of $\triangle ABC, O$ be the circumcenter of $\triangle ABC.$

It is clear that $Go$ is the midpoint of $AA'.$ $M = A'C' \cap AB$ is the midpoint $AB, N = A'B' \cap AC$ is the midpoint $AC.$

$\triangle A'BM = \triangle CNA' \sim \triangle CBA$ with coefficient $k = \frac {1}{2}.$

Any equilateral triangle and its Gossard triangle are congruent.

Any equilateral triangle and its Gossard triangle have the same Euler line.

The Gossard triangle of the equilateral $\triangle ABC$ is the reflection of $\triangle ABC$ in the Gossard perspector. Denote $\angle BAC = \alpha, \angle ABC = \angle ACB = \beta, AO = BO = R \implies$ \[\sin \beta = \cos \frac {\alpha}{2}, GoO = AO – AGo = R \cdot \frac{1 – \cos {\alpha}}{2},\] \[OH = AH – AO = R(2 \cos \alpha – 1) \implies \vec {GoO} = \vec {OH} \cdot \frac {1 – \cos \alpha}{2(2 \cos \alpha – 1)}.\]

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Gossard_perspector&oldid=186234"