Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Simson line"

(→‎Simson line (main))
(→‎Simson line (main))
Line 5: Line 5:
 
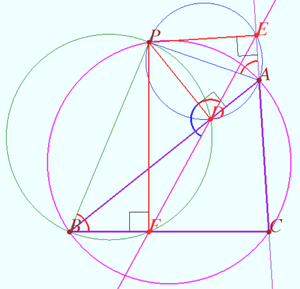
In the shown diagram, we draw additional lines <math>AP</math> and <math>BP</math>. Then, we have cyclic quadrilaterals <math>ACBP</math>, <math>PC_1A_1B</math>, and <math>PB_1AC_1</math>. (more will be added)
 
In the shown diagram, we draw additional lines <math>AP</math> and <math>BP</math>. Then, we have cyclic quadrilaterals <math>ACBP</math>, <math>PC_1A_1B</math>, and <math>PB_1AC_1</math>. (more will be added)
 
==Simson line (main)==
 
==Simson line (main)==
−
[[File:Simson line.png|350px|right]]
+
[[File:Simson line.png|300px|right]]
 
Let a triangle <math>\triangle ABC</math> and a point <math>P</math> be given. Let <math>D, E,</math> and <math>F</math> be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.
 
Let a triangle <math>\triangle ABC</math> and a point <math>P</math> be given. Let <math>D, E,</math> and <math>F</math> be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.
  
Line 18: Line 18:
 
<math>ACBP</math> is cyclic <math>\implies \angle PBC = \angle PAE \implies \angle PDF + \angle PDE = 180^\circ</math>
 
<math>ACBP</math> is cyclic <math>\implies \angle PBC = \angle PAE \implies \angle PDF + \angle PDE = 180^\circ</math>
 
<math>\implies D, E,</math> and <math>F</math> are collinear as desired.  
 
<math>\implies D, E,</math> and <math>F</math> are collinear as desired.  
 +
 +
<i><b>Proof</b></i>
  
 
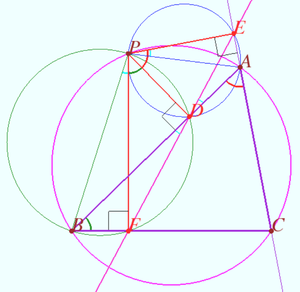
Let the points  <math>D, E,</math> and <math>F</math> be collinear.  
 
Let the points  <math>D, E,</math> and <math>F</math> be collinear.  
−
[[File:Simson line inverse.png|350px|right]]
+
[[File:Simson line inverse.png|300px|right]]
 
<math>AEPD</math> is cyclic <math>\implies \angle APE = \angle ADE, \angle APE = \angle BAC.</math>  
 
<math>AEPD</math> is cyclic <math>\implies \angle APE = \angle ADE, \angle APE = \angle BAC.</math>  
 
<math>BFDP</math> is cyclic <math>\implies \angle BPF = \angle BDF, \angle DPF = \angle ABC.</math>
 
<math>BFDP</math> is cyclic <math>\implies \angle BPF = \angle BDF, \angle DPF = \angle ABC.</math>

Revision as of 14:45, 30 November 2022

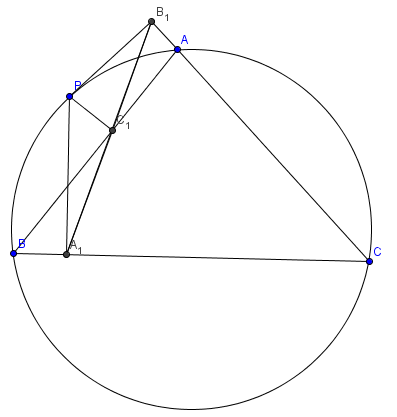
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. Simsonline.png

Proof

In the shown diagram, we draw additional lines $AP$ and $BP$. Then, we have cyclic quadrilaterals $ACBP$, $PC_1A_1B$, and $PB_1AC_1$. (more will be added)

Simson line (main)

Simson line.png

Let a triangle $\triangle ABC$ and a point $P$ be given. Let $D, E,$ and $F$ be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.

Then points $D, E,$ and $F$ are collinear iff the point $P$ lies on circumcircle of $\triangle ABC.$

Proof

Let the point $P$ be on the circumcircle of $\triangle ABC.$ $\angle BFP = \angle BDP = 90^\circ \implies BPDF$ is cyclic $\implies \angle PDF = 180^\circ – \angle CBP.$ $\angle ADP = \angle AEP = 90^\circ \implies AEPD$ is cyclic $\implies \angle PDE = \angle PAE.$

$ACBP$ is cyclic $\implies \angle PBC = \angle PAE \implies \angle PDF + \angle PDE = 180^\circ$ $\implies D, E,$ and $F$ are collinear as desired.

Proof

Let the points $D, E,$ and $F$ be collinear.

Simson line inverse.png

$AEPD$ is cyclic $\implies \angle APE = \angle ADE, \angle APE = \angle BAC.$ $BFDP$ is cyclic $\implies \angle BPF = \angle BDF, \angle DPF = \angle ABC.$

$\angle ADE = \angle BDF \implies \angle BPA = \angle EPF$ $= \angle BAC + \angle ABC = 180^\circ – \angle ACB \implies ACBP$ is cyclis as desired.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Simson_line&oldid=183349"