Difference between revisions of "De Longchamps point"

Revision as of 07:53, 16 November 2022

The title of this article has been capitalized due to technical restrictions. The correct title should be 'de Longchamps point'.

$[asy] draw((0,0)--(44,60)--(44,-10)--cycle); draw((0,0)--(44,0),blue+dashed); draw((44,60)--(22,-5),blue+dashed); draw((44,-10)--(6.5,10),blue+dashed); label("H",(24,0),(1,1)); dot((24,0)); draw((22,30)--(44,14),red); draw((22,-5)--(34,46),red); draw((44,25)--(18,25),red); dot((29,25)); label("C",(29,25),(1,1)); draw(Circle((29,25),25),dashed); dot((34,50)); label("L",(34,50),(1,1)); [/asy]$

The de Longchamps
point ( $L$ ) is the the
orthocenter ( $H$ ) reflected
through the circumcenter
( $C$ ).

The de Longchamps point of a triangle is the reflection of the triangle's orthocenter through its circumcenter.

The point is collinear with the orthocenter and circumcenter.

de Longchamps point

Definition 1

The de Longchamps point of a triangle is the radical center of the power circles of the triangle. Prove that De Longchamps point lies on Euler line.

We call A-power circle of a $\triangle ABC$ the circle centered at the midpoint $BC$ point $A'$ with radius $R_A = AA'.$ The other two circles are defined symmetrically.

Proof

Let $H, O,$ and $L$ be orthocenter, circumcenter, and De Longchamps point, respectively.

Denote $B-$ power circle by $\omega_B, C-$ power circle by $\omega_C, D = \omega_B \cap \omega_C,$ $a = BC, b = AC, c = AB.$ WLOG, $a \ge b \ge c.$

Denote $X_t$ the projection of point $X$ on $B'C', E = D_t.$

We will prove that radical axes of $B-$ power and $C-$ power cicles is symmetric to altitude $AH$ with respect $O.$ Further, we will conclude that the point of intersection of the radical axes, symmetrical to the heights with respect to O, is symmetrical to the point of intersection of the heights $H$ with respect to $O.$

Point $E$ is the crosspoint of the center line of the $B-$ power and $C-$ power circles and there radical axis. $B'C' = \frac {a}{2}.$ We use claim and get:

$C'E = \frac {a}{4} + \frac {R_C^2 – R_B^2}{a}.$ $R_B$ and $R_C$ are the medians, so $R_B^2 = \frac {a^2}{2}+ \frac {c^2}{2} – \frac {b^2}{4}, R_C^2 = \frac {a^2}{2}+ \frac {b^2}{2} – \frac {c^2}{4} \implies C'E = \frac {a}{4} + \frac {3(b^2 – c^2)}{4a}.$

We use Claim some times and get: $C'A_t = \frac {a}{4} – \frac {b^2 – c^2}{4a}, A_tO_t = \frac {a}{2} – 2 C'A_t = \frac {b^2 – c^2}{2a} \implies$ $O_t L_t = C'E – C'A_t - A_t O_t = \frac {b^2 – c^2}{2a} = A_t O_t = H_t O_t \implies$ radical axes of $B-$ power and $C-$ power cicles is symmetric to altitude $AH$ with respect $O.$

Similarly radical axes of $A-$ power and $B-$ power cicles is symmetric to altitude $CH,$ radical axes of $A-$ power and $C-$ power cicles is symmetric to altitude $BH$ with respect $O.$ Therefore the point $L$ of intersection of the radical axes, symmetrical to the heights with respect to $O,$ is symmetrical to the point $H$ of intersection of the heights with respect to $O \implies \vec {HO} = \vec {OL} \implies L$ lies on Euler line of $\triangle ABC.$

Claim (Distance between projections)

$x + y = a, c^2 – x^2 = h^2 = b^2 – y^2,$ $y^2 – x^2 = b^2 – c^2 \implies y – x = \frac {b^2 – c^2}{a},$ $x = \frac {a}{2} – \frac {b^2 – c^2}{2a}, y = \frac {a}{2} + \frac {b^2 – c^2}{2a}.$

Definition 2

We call $\omega_A = A-$ circle of a $\triangle ABC$ the circle centered at $A$ with radius $BC.$ The other two circles are defined symmetrically. The De Longchamps point of a triangle is the radical center of $A-$ circle, $B-$ circle, and $C-$ circle of the triangle (Casey – 1886). Prove that De Longchamps point under this definition is the same as point under Definition 1.

Proof

Let $H, G,$ and $L_o$ be orthocenter, centroid, and De Longchamps point, respectively. Let $\omega_B$ cross $\omega_C$ at points $A'$ and $E.$ The other points $(D, F, B', C')$ are defined symmetrically. $AB' = BC, B'C = AB \implies \triangle ABC = \triangle CB'A \implies$ $AB||B'C \implies CH \perp B'C.$ Similarly $CH \perp A'C \implies A'B'$ is diameter $\omega_C \implies$ $\angle A'EB' = 90^\circ, 2\vec {BG} = \vec {GB'}.$

Therefore $\triangle A'B'C'$ is anticomplementary triangle of $\triangle ABC, \triangle DEF$ is orthic triangle of $\triangle A'B'C'.$ So $L_o$ is orthocenter of $\triangle A'B'C'.$

$2\vec {HG} = \vec GL_o, 2\vec {GO} = \vec HG \implies L_o = L$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

De Longchamps circle

De Longchamps circle $\Omega$ of the obtuse triangle $ABC$ is circle centered at de Longchamps point $L$ which is orthogonal to the $\omega_C.$ Prove that de Longchamps circle is orthogonal to the $\omega_A, \omega_B, A-$ power, $B-$ power and $C-$ power cicles and the radius of de Longchamps circle is $R_{\Omega} = 4R \sqrt { – \cos A \cos B \cos C}.$

Proof

$\vec {A'B'} = 2\vec {BA}, A'B'$ – diameter $\omega_C.$

Let $E$ be the foot of perpendicular from $L$ to $AB'.$

Let $E_0$ be crosspoint of $\omega_C$ and $AB' \implies A'E_0 \perp AB' \implies E = E_0.$

Points $A'$ and $E$ are simmetric with respect to $BC, MA' = AM \implies$

Points $A'$ and $E$ lies on $A-$ power circle and on $\omega_C$ .

$\Omega \perp \omega_C,$ points $L, A',$ and $E$ are collinear $\implies \Omega \perp A-$ power circle.

$L$ is the radical center of all six circles, therefore $\Omega$ is perpendicular to each of these circles. $L$ is orthocenter of the anticomplementary triangle of $\triangle ABC$ so radius of $\Omega$ is twice radius of circle finded by Claim $\implies R_{\Omega} = 4R \sqrt { – \cos A \cos B \cos C}.$

Claim (Radius)

Let $ABC$ be obtuse triangle $(\angle A > 90^\circ)$ with circumcircle $\Omega,$ circumradius $R,$ and orthocenter $H.$ Let $\omega'$ be the circle with diameter $AB.$ Let $\omega$ be the circle perpendicular to $\omega'$ centered at $H.$ Find $R_\omega,$ the radius of $\omega.$

Let altitude $AH$ cross $BC$ at $D$ and cross $\Omega$ second time at $H'.$ $AD \perp BD \implies D \in \omega',$ points $H,A, D$ are collinear $\implies$ inversion with respect $\omega$ swap $A$ and $D \implies R_\omega^2 = HA \cdot HD.$ Well known that $HA = – 2R \cos A.$ $BC \perp HD, AC \perp BH \implies \angle C = \angle BHD \implies HD = BH \cos C.$ Points $H$ and $H'$ are symmetric with respect $BC \implies BH' = BH.$ $\angle BAH' = 90^\circ – \angle B \implies BH' = 2R \sin \angle BAH' = 2R \cos B \implies$ $R_\omega^2 = – 2R \cos A \cdot 2R \cos B \cos C \implies R_\omega = 2R \sqrt{– \cos A \cos B \cos C}.$

vladimir.shelomovskii@gmail.com, vvsss

@@ Line 75: / Line 75: @@
 <math>2\vec {HG} = \vec GL_o, 2\vec {GO} = \vec HG \implies L_o = L</math> as desired.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==De Longchamps circle==
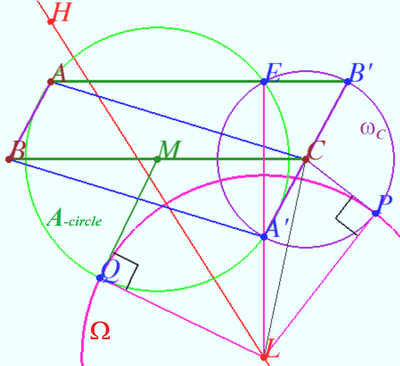
+[[File:Longchamps circle.png|400px|right]]
+De Longchamps circle <math>\Omega</math> of the obtuse triangle <math>ABC</math> is circle centered at de Longchamps point <math>L</math> which is orthogonal to the <math>\omega_C.</math> Prove that de Longchamps circle is orthogonal to the <math>\omega_A, \omega_B, A-</math>power, <math>B-</math>power and <math>C-</math>power cicles and the radius of de Longchamps circle is <math>R_{\Omega} = 4R \sqrt { – \cos A \cos B \cos C}.</math>
+<i><b>Proof</b></i>
+<math>\vec {A'B'} = 2\vec {BA}, A'B'</math> – diameter <math>\omega_C.</math>
+Let <math>E</math> be the foot of perpendicular from <math>L</math> to <math>AB'.</math>
+Let <math>E_0</math> be crosspoint of <math>\omega_C</math> and <math>AB' \implies A'E_0 \perp AB' \implies E = E_0.</math>
+Points <math>A'</math> and <math>E</math> are simmetric with respect to <math>BC, MA' = AM \implies</math>
+Points <math>A'</math> and <math>E</math> lies on <math>A-</math>power circle and on <math>\omega_C</math>.
+<math>\Omega \perp \omega_C,</math> points <math>L, A',</math> and <math>E</math> are collinear <math>\implies \Omega \perp A-</math> power circle.
+<math>L</math> is the radical center of all six circles, therefore <math>\Omega</math> is perpendicular to each of these circles.
+<math>L</math> is orthocenter of the anticomplementary triangle of <math>\triangle ABC</math> so radius of <math>\Omega</math> is twice radius of circle finded by Claim <math>\implies R_{\Omega} = 4R \sqrt { – \cos A \cos B \cos C}.</math>
+<i><b>Claim (Radius)</b></i>
+Let <math>ABC</math> be obtuse triangle <math>(\angle A > 90^\circ)</math> with circumcircle <math>\Omega,</math> circumradius <math>R,</math> and orthocenter <math>H.</math>
+Let <math>\omega'</math> be the circle with diameter <math>AB.</math>
+Let <math>\omega</math> be the circle perpendicular to <math>\omega'</math> centered at <math>H.</math> Find <math>R_\omega,</math> the radius of <math>\omega.</math>
+Let altitude <math>AH</math> cross <math>BC</math> at <math>D</math> and cross <math>\Omega</math> second time at <math>H'.</math>
+<math>AD \perp BD \implies D \in \omega',</math> points <math>H,A, D</math> are collinear <math>\implies</math> inversion with respect <math>\omega</math> swap <math>A</math> and <math>D \implies R_\omega^2 = HA \cdot HD.</math>
+Well known that <math>HA = – 2R \cos A.</math>
+<cmath>BC \perp HD, AC \perp BH \implies \angle C = \angle BHD \implies HD = BH \cos C.</cmath>
+Points <math>H</math> and <math>H'</math> are symmetric with respect <math>BC \implies BH' = BH.</math>
+<cmath>\angle BAH' = 90^\circ – \angle B \implies BH' = 2R \sin \angle BAH' = 2R \cos B \implies</cmath>
+<cmath>R_\omega^2 = – 2R \cos A \cdot 2R \cos B \cos C \implies R_\omega = 2R \sqrt{– \cos A \cos B \cos C}.</cmath>
 '''vladimir.shelomovskii@gmail.com, vvsss'''

Page

Toolbox

Search

Difference between revisions of "De Longchamps point"

Revision as of 07:53, 16 November 2022

de Longchamps point

De Longchamps circle

See Also