Difference between revisions of "1989 AIME Problems/Problem 15"
(→See also) |
(→See also) |
||
| Line 8: | Line 8: | ||
== See also == | == See also == | ||
| − | {{AIME box|year=1989|num-b=14|after=Final | + | {{AIME box|year=1989|num-b=14|after=Final Question}} |
Revision as of 07:50, 15 October 2007
Problem
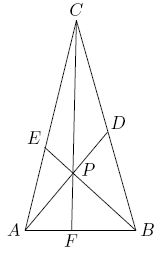
Point 
is inside 
. Line segments 
, 
, and 
are drawn with 
on 
, 
on 
, and 
on 
(see the figure at right). Given that 
, 
, 
, 
, and 
, find the area of .
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Final Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
