Difference between revisions of "1989 AIME Problems/Problem 12"
m |
(→See also) |
||
| Line 8: | Line 8: | ||
== See also == | == See also == | ||
| − | + | {{AIME box|year=1989|num-b=11|num-a=13}} | |
| − | |||
| − | |||
Revision as of 07:42, 15 October 2007
Problem
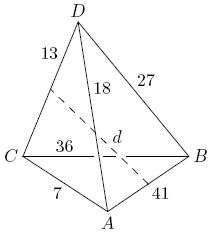
Let 
be a tetrahedron with 
, 
, 
, 
, 
, and 
, as shown in the figure. Let 
be the distance between the midpoints of edges 
and 
. Find 
.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
