Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AMC 10A Problems/Problem 19"

m
(add alternate solution without casework)
Line 5: Line 5:
  
 
== Solution 1 ==
 
== Solution 1 ==
−
In order to attack this problem, we need to consider casework:
+
In order to attack this problem, we can use casework on the sign of <math>|x-y|</math> and <math>|x+y|</math>.
  
 
Case 1: <math>|x-y|=x-y, |x+y|=x+y</math>
 
Case 1: <math>|x-y|=x-y, |x+y|=x+y</math>
Line 42: Line 42:
 
~Bryguy
 
~Bryguy
  
−
==Solution 2 (Guessing)==
+
==Solution 2 ==
 +
A somewhat faster variant of solution 1 is to use a bit of symmetry in order to show that the remaining three cases are identical to Case 1 in the above solution, up to rotations by <math>90^{\circ}</math> about the origin. This allows us to quickly sketch the region after solving Case 1.
 +
 
 +
Upon simplifying Case 1, we obtain <math>(x-3)^2 + y^2 = 3^2</math> which is a circle of radius 3 centered at <math>(3,0)</math> We remark that only the points on the semicircle where <math>x \ge 3</math> work, since Case 1 assumes <math>x-y \ge 0</math> and <math>x+y \ge 0</math>. Let <math>(x_0,y_0)</math> be an arbitrary point in the Cartesian plane, and let <math>(x_1,y_1)</math> be a point obtained by rotations of <math>90^{\circ}</math> about the origin such that <math>(x_1,y_1)</math> satisfies the conditions of Case 1.
 +
 
 +
We claim that <math>(x_0,y_0)</math> is a solution to the given equation if and only if <math>(x_1,y_1)</math> is also a solution. The proof is to note that rotation by <math>90^{\circ}</math> about the origin preserves both the value of <math>x^2+y^2</math> (as the distance to the origin is the same), as well as the value of <math>|x-y|+|x+y|</math> (as this represents the sum of distances from a point to the lines <math>y=x</math> and <math>y=-x</math>, multiplied by <math>\sqrt{2}</math>). Therefore the value of <math>x^2+y^2 - 3(|x-y|+|x+y|)</math> is invariant to rotations by <math>90^{\circ}</math>, establishing the claim.
 +
We obtain <math>\boxed{(E) 54}</math> as above.
 +
 
 +
~scrabbler94
 +
 
 +
==Solution 3 (Guessing)==
 
Assume <math>y</math> = <math>0</math>. We get that <math>x</math> = <math>6</math>. That means that this figure must contain the points <math>(0,6), (6,0), (0, -6), (-6, 0)</math>. Now, assume that <math>x</math> = <math>y</math>. We get that <math>x</math> = <math>3 \sqrt 3</math>. We get the points <math>(3,3), (3,-3), (-3, 3), (-3, -3)</math>.  
 
Assume <math>y</math> = <math>0</math>. We get that <math>x</math> = <math>6</math>. That means that this figure must contain the points <math>(0,6), (6,0), (0, -6), (-6, 0)</math>. Now, assume that <math>x</math> = <math>y</math>. We get that <math>x</math> = <math>3 \sqrt 3</math>. We get the points <math>(3,3), (3,-3), (-3, 3), (-3, -3)</math>.  
  

Revision as of 05:13, 28 October 2022

Problem

The area of the region bounded by the graph of\[x^2+y^2 = 3|x-y| + 3|x+y|\]is $m+n\pi$, where $m$ and $n$ are integers. What is $m + n$?

$\textbf{(A)} ~18\qquad\textbf{(B)} ~27\qquad\textbf{(C)} ~36\qquad\textbf{(D)} ~45\qquad\textbf{(E)} ~54$

Solution 1

In order to attack this problem, we can use casework on the sign of $|x-y|$ and $|x+y|$.

Case 1: $|x-y|=x-y, |x+y|=x+y$

Substituting and simplifying, we have $x^2-6x+y^2=0$, i.e. $(x-3)^2+y^2=3^2$, which gives us a circle of radius $3$ centered at $(3,0)$.

Case 2: $|x-y|=y-x, |x+y|=x+y$

Substituting and simplifying again, we have $x^2+y^2-6y=0$, i.e. $x^2+(y-3)^2=3^2$. This gives us a circle of radius $3$ centered at $(0,3)$.

Case 3: $|x-y|=x-y, |x+y|=-x-y$

Doing the same process as before, we have $x^2+y^2+6y=0$, i.e. $x^2+(y+3)^2=3^2$. This gives us a circle of radius $3$ centered at $(0,-3)$.

Case 4: $|x-y|=y-x, |x+y|=-x-y$

One last time: we have $x^2+y^2+6x=0$, i.e. $(x+3)^2+y^2=3^2$. This gives us a circle of radius $3$ centered at $(-3,0)$.

After combining all the cases and drawing them on the Cartesian Plane, this is what the diagram looks like:

[asy] size(10cm); Label f; f.p=fontsize(7); xaxis(-8,8,Ticks(f, 1.0)); yaxis(-8,8,Ticks(f, 1.0)); draw(arc((-3,0),3,90,270) -- cycle, gray); draw(arc((0,3),3,0,180) -- cycle, gray); draw(arc((3,0),3,-90,90) -- cycle, gray); draw(arc((0,-3),3,-180,0) -- cycle, gray); draw((-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle, grey); [/asy] Now, the area of the shaded region is just a square with side length $6$ with four semicircles of radius $3$. The area is $6\cdot6+4\cdot \frac{9\pi}{2} = 36+18\pi$. The answer is $36+18$ which is $\boxed{\textbf{(E) }54}$

~Bryguy

Solution 2

A somewhat faster variant of solution 1 is to use a bit of symmetry in order to show that the remaining three cases are identical to Case 1 in the above solution, up to rotations by $90^{\circ}$ about the origin. This allows us to quickly sketch the region after solving Case 1.

Upon simplifying Case 1, we obtain $(x-3)^2 + y^2 = 3^2$ which is a circle of radius 3 centered at $(3,0)$ We remark that only the points on the semicircle where $x \ge 3$ work, since Case 1 assumes $x-y \ge 0$ and $x+y \ge 0$. Let $(x_0,y_0)$ be an arbitrary point in the Cartesian plane, and let $(x_1,y_1)$ be a point obtained by rotations of $90^{\circ}$ about the origin such that $(x_1,y_1)$ satisfies the conditions of Case 1.

We claim that $(x_0,y_0)$ is a solution to the given equation if and only if $(x_1,y_1)$ is also a solution. The proof is to note that rotation by $90^{\circ}$ about the origin preserves both the value of $x^2+y^2$ (as the distance to the origin is the same), as well as the value of $|x-y|+|x+y|$ (as this represents the sum of distances from a point to the lines $y=x$ and $y=-x$, multiplied by $\sqrt{2}$). Therefore the value of $x^2+y^2 - 3(|x-y|+|x+y|)$ is invariant to rotations by $90^{\circ}$, establishing the claim. We obtain $\boxed{(E) 54}$ as above.

~scrabbler94

Solution 3 (Guessing)

Assume $y$ = $0$. We get that $x$ = $6$. That means that this figure must contain the points $(0,6), (6,0), (0, -6), (-6, 0)$. Now, assume that $x$ = $y$. We get that $x$ = $3 \sqrt 3$. We get the points $(3,3), (3,-3), (-3, 3), (-3, -3)$.

Since this contains $x^2 + y^2$, assume that there are circles. Therefore, we can guess that there is a center square with area $6 \cdot 6$ = $36$ and $4$ semicircles with radius $3$. We get $4$ semicircles with area $4.5 \pi$, and therefore the answer is $36+18$ = $\boxed {(E)54}$

~Arcticturn

Remark

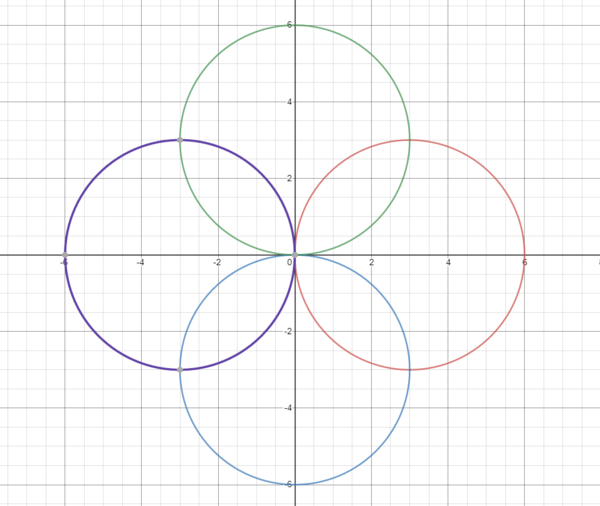
This problem asks for the area of the union of these four circles:

Image 2021-02-11 111327.png

Video Solution (Using Absolute Value Properties to Graph)

https://youtu.be/EHHpB6GIGPc

~ pi_is_3.14

Video Solution by The Power Of Logic (Graphing)

https://youtu.be/-pa72wBA85Y

Video Solution by TheBeautyofMath

https://youtu.be/U6obY_kio0g

~IceMatrix

See Also

2021 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 18 		Followed by
Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AMC_10A_Problems/Problem_19&oldid=179596"