Difference between revisions of "Kimberling’s point X(24)"
(Kimberling’s point X(24)) |
|||
| Line 1: | Line 1: | ||
| + | <i><b> Kimberling point X(24) </b></i> | ||
| + | [[File:2016 USAMO 3g.png|450px|right]] | ||
| + | |||
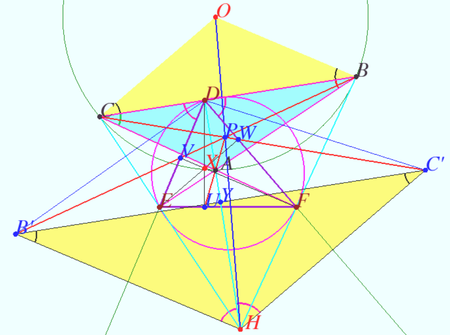
| + | Perspector of Triangle <math>ABC</math> and Orthic Triangle of the Orthic Triangle. | ||
| + | <i><b>Theorem 1</b></i> | ||
| + | Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of the Orthic Triangle of <math>T_0</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math> | ||
| + | |||
| + | Then <math>\triangle T_0</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line <math>OH</math> of <math>T_0.</math> | ||
| + | |||
| + | The ratio of the homothety is <math>k = \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | WLOG, we use case <math>\angle A = \alpha > 90^\circ.</math> | ||
| + | Let <math>B'</math> be reflection <math>H</math> in <math>DE.</math> | ||
| + | |||
| + | In accordance with Claim, <math>\angle BVD = \angle HVE \implies B', V,</math> and <math>B</math> are collinear. | ||
| + | |||
| + | Similarly, <math>C, W,</math> and <math>C',</math> were <math>C'</math> is reflection <math>H</math> in <math>DF,</math> are collinear. | ||
| + | |||
| + | Denote <math>\angle ABC = \beta = \angle CHD, \angle ACB = \gamma = \angle BHD \implies</math> | ||
| + | |||
| + | <math>\angle HDF = \angle HDE = \angle DHB' = \angle DHC' = 180^\circ - \alpha.</math> | ||
| + | |||
| + | <math>B'C' \perp HD, BC \perp HD \implies BC|| B'C'.</math> | ||
| + | <math>OB = OC, HB' = HC', \angle BOC = \angle B'HC' = 360^\circ - 2 \alpha \implies OB ||HB', OC || HC' \implies</math> | ||
| + | |||
| + | <math>\triangle HB'C' \sim \triangle OBC, BB', CC'</math> and <math>HO</math> are concurrent at point <math>P.</math> | ||
| + | |||
| + | In accordance with Claim, <math>\angle HUF = \angle AUF \implies</math> points <math>H</math> and <math>P</math> are isogonal conjugate with respect <math>\triangle UVW.</math> | ||
| + | |||
| + | <math>\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies</math> | ||
| + | |||
| + | <math>HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.</math> | ||
| + | <math>k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.</math> | ||
| + | |||
| + | <i><b>Claim</b></i> | ||
| + | [[File:2016 3 Lemma.png|400px|right]] | ||
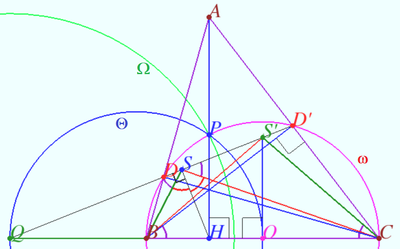
| + | Let <math>\triangle ABC</math> be an acute triangle, and let <math>AH, BD',</math> and <math>CD</math> denote its altitudes. Lines <math>DD'</math> and <math>BC</math> meet at <math>Q, HS \perp DD'.</math> Prove that <math>\angle BSH = \angle CSH.</math> | ||
| − | + | <i><b>Proof</b></i> | |
| − | + | ||
| − | + | Let <math>\omega</math> be the circle <math>BCD'D</math> centered at <math>O (O</math> is midpoint <math>BC).</math> | |
| + | |||
| + | Let <math>\omega</math> meet <math>AH</math> at <math>P.</math> | ||
| + | Let <math>\Omega</math> be the circle centered at <math>Q</math> with radius <math>QP.</math> | ||
| + | |||
| + | Let <math>\Theta</math> be the circle with diameter <math>OQ.</math> | ||
| + | |||
| + | We know that <math>OB = OP = OC = R, PH^2 = R^2 – OH^2 \implies</math> | ||
| + | <math>QP^2 + R^2 = (QH+ HO)^2 \implies P \in \Theta, \Omega \perp \omega.</math> | ||
| + | |||
| + | Let <math>I_{\Omega}</math> be inversion with respect <math>\Omega, I_{\Omega}(B) = C.</math> | ||
| + | |||
| + | Denote <math>I_{\Omega}(D) = D', I_{\Omega}(S) = S',</math> | ||
| + | <math>QH \cdot QO = QP^2 \implies I_{\Omega}(H) = O.</math> | ||
| + | <math>HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.</math> | ||
| + | |||
| + | <math>\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.</math> | ||
| + | |||
| + | <math>\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.</math> | ||
| + | |||
| + | <i><b>Theorem 2</b></i> | ||
| + | |||
| + | Let <math>T_0 = \triangle ABC</math> be the base triangle, <math>T_1 = \triangle DEF</math> be orthic triangle of <math>T_0, T_2 = \triangle KLM</math> be Kosnita triangle. Then <math>\triangle T_1</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line of <math>T_0,</math> the ratio of the homothety is <math>k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.</math> | ||
| + | We recall that vertex of Kosnita triangle are: <math>K</math> is the circumcenter of <math>\triangle OBC, L</math> is the circumcenter of <math>\triangle OAB, M</math> is the circumcenter of <math>\triangle OAC,</math> where <math>O</math> is circumcenter of <math>T_0.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 07:50, 12 October 2022
Kimberling point X(24)
Perspector of Triangle ![]() and Orthic Triangle of the Orthic Triangle.
Theorem 1
Denote
and Orthic Triangle of the Orthic Triangle.
Theorem 1
Denote ![]() obtuse or acute
obtuse or acute ![]() Let
Let ![]() be the base triangle,
be the base triangle, ![]() be Orthic triangle of
be Orthic triangle of ![]() be Orthic Triangle of the Orthic Triangle of
be Orthic Triangle of the Orthic Triangle of ![]() . Let
. Let ![]() and
and ![]() be the circumcenter and orthocenter of
be the circumcenter and orthocenter of ![]()
Then ![]() and
and ![]() are homothetic, the point
are homothetic, the point ![]() center of this homothety lies on Euler line
center of this homothety lies on Euler line ![]() of
of ![]()
The ratio of the homothety is ![]()
Proof
WLOG, we use case ![]() Let
Let ![]() be reflection
be reflection ![]() in
in ![]()
In accordance with Claim, ![]() and
and ![]() are collinear.
are collinear.
Similarly, ![]() and
and ![]() were
were ![]() is reflection
is reflection ![]() in
in ![]() are collinear.
are collinear.
Denote ![]()
![]()
![]()
![]()
![]() and
and ![]() are concurrent at point
are concurrent at point ![]()
In accordance with Claim, ![]() points
points ![]() and
and ![]() are isogonal conjugate with respect
are isogonal conjugate with respect ![]()
![]()
![]()
![]()
Claim
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its altitudes. Lines
denote its altitudes. Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]()
Proof
Let ![]() be the circle
be the circle ![]() centered at
centered at ![]() is midpoint
is midpoint ![]()
Let ![]() meet
meet ![]() at
at ![]() Let
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
Let ![]() be the circle with diameter
be the circle with diameter ![]()
We know that ![]()
![]()
Let ![]() be inversion with respect
be inversion with respect ![]()
Denote ![]()
![]()
![]()
![]()
![]()
Theorem 2
Let ![]() be the base triangle,
be the base triangle, ![]() be orthic triangle of
be orthic triangle of ![]() be Kosnita triangle. Then
be Kosnita triangle. Then ![]() and
and ![]() are homothetic, the point
are homothetic, the point ![]() center of this homothety lies on Euler line of
center of this homothety lies on Euler line of ![]() the ratio of the homothety is
the ratio of the homothety is ![]() We recall that vertex of Kosnita triangle are:
We recall that vertex of Kosnita triangle are: ![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]() where
where ![]() is circumcenter of
is circumcenter of ![]()
vladimir.shelomovskii@gmail.com, vvsss