Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 USAMO Problems/Problem 3"

(→‎Solution)
(→‎Solution)
Line 48: Line 48:
 
<math>\angle XN'I' = \angle XSI' = 90^\circ – \angle AXI' = \angle IFX \implies N'XIF</math> is cyclic.  
 
<math>\angle XN'I' = \angle XSI' = 90^\circ – \angle AXI' = \angle IFX \implies N'XIF</math> is cyclic.  
  
−
<math>I_\omega (NAI'M) = N'XIKF \implies I_\omega(F) = L \implies</math> the points <math>F, L,</math> and <math>S</math> are collinear.
+
Therefore point <math>F</math> lies on  <math>I_\omega (AMN) \implies I_\omega(F) = L \implies</math>
 +
The points <math>F, L,</math> and <math>S</math> are collinear.
  
−
Point <math>I</math> is orthocenter <math>\triangle FSX \implies XI \perp SF, \angle ILS = \angle SI'F = 90^\circ \implies</math> the points <math>X, I, E,</math> and <math>L</math> are collinear.
+
Point <math>I</math> is orthocenter <math>\triangle FSX \implies XI \perp SF, \angle ILS = \angle SI'F = 90^\circ \implies</math>
 +
The points <math>X, I, E,</math> and <math>L</math> are collinear.
  
 
<math>SAI'F = I_\omega (XIF) \implies AI \cdot IF = SI \cdot II' = AI \cdot \frac {IF}{2} = \frac {SI}{2} \cdot II' = AI \cdot IM = EI \cdot IX \implies AEMX</math> is cyclic.
 
<math>SAI'F = I_\omega (XIF) \implies AI \cdot IF = SI \cdot II' = AI \cdot \frac {IF}{2} = \frac {SI}{2} \cdot II' = AI \cdot IM = EI \cdot IX \implies AEMX</math> is cyclic.

Revision as of 08:27, 21 September 2022

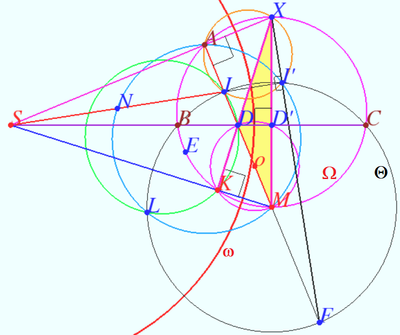
Problem

Let $ABC$ be a scalene triangle with circumcircle $\Omega$ and incenter $I.$ Ray $AI$ meets $BC$ at $D$ and $\Omega$ again at $M;$ the circle with diameter $DM$ cuts $\Omega$ again at $K.$ Lines $MK$ and $BC$ meet at $S,$ and $N$ is the midpoint of $IS.$ The circumcircles of $\triangle KID$ and $\triangle MAN$ intersect at points $L_1$ and $L.$ Prove that $\Omega$ passes through the midpoint of either $IL_1$ or $IL.$

Solution

2017 USAMO 3.png
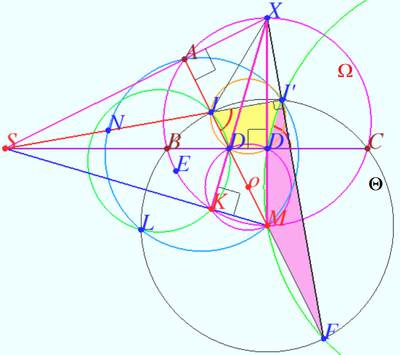
2017 USAMO 3a.png

Let $X$ be the point on circle $\Omega$ opposite $M \implies \angle MAX = 90^\circ, BC \perp XM.$

$\angle XKM = \angle DKM = 90^\circ \implies$ the points $X, D,$ and $K$ are collinear.

Let $D' = BC \cap XM \implies DD' \perp XM \implies$

$S$ is the orthocenter of $\triangle DMX \implies$ the points $X, A,$ and $S$ are collinear.

Let $\omega$ be the circle centered at $S$ with radius $R = \sqrt {SK \cdot SM}.$

We denote $I_\omega$ inversion with respect to $\omega.$

Note that the circle $\Omega$ has diameter $MX$ and contain points $A, B, C,$ and $K.$

$I_\omega (K) = M \implies$ circle $\Omega \perp \omega \implies C = I_\omega (B), X = I_\omega (A).$

$I_\omega (K) = M \implies$ circle $KMD \perp \omega \implies D' = I_\omega (D) \in KMD \implies$ $\angle DD'M = 90^\circ \implies$ the points $X, D',$ and $M$ are collinear.

Let $F \in AM, MF = MI.$ It is well known that $MB = MI = MC \implies$

$\Theta = BICF$ is circle centered at $M.$ $C = I_\omega (B) \implies \Theta \perp \omega.$

Let $I' = I_\omega (I ) \implies I' \in \Theta \implies \angle II'M = 90^\circ.$ $I' = I_\omega (I ), X = I_\omega (A ) \implies AII'X$ is cyclic.

$\angle XI'I = \angle XAI = 90^\circ \implies$ the points $X, I' ,$ and $F$ are collinear.

$I'IDD'$ is cyclic $\implies \angle I'D'M = \angle I'D'C + 90^\circ = \angle I'ID + 90^\circ,$ $\angle XFM = \angle I'FI = 90^\circ – \angle I'IF = 90^\circ – \angle I'ID \implies$

$\angle XFM + \angle I'D'M = 180^\circ \implies I'D'MF$ is cyclic.

Therefore point $F$ lies on $I_\omega (IDK).$

$FA \perp SX, SI' \perp FX \implies I$ is orthocenter of $\triangle FSX.$

$N$ is midpoint $SI, M$ is midpoint $FI, I$ is orthocenter of $\triangle FSX, A$ is root of height $FA \implies AMN$ is the nine-point circle of $\triangle FSX \implies I' \in AMN.$

Let $N' = I_\omega (N) \implies R^2 = SN \cdot SN' = SI \cdot SI' \implies$ \[\frac {SN'}{SI'} = \frac {SI}{SN} =2 \implies\] $\angle XN'I' = \angle XSI' = 90^\circ – \angle AXI' = \angle IFX \implies N'XIF$ is cyclic.

Therefore point $F$ lies on $I_\omega (AMN) \implies I_\omega(F) = L \implies$ The points $F, L,$ and $S$ are collinear.

Point $I$ is orthocenter $\triangle FSX \implies XI \perp SF, \angle ILS = \angle SI'F = 90^\circ \implies$ The points $X, I, E,$ and $L$ are collinear.

$SAI'F = I_\omega (XIF) \implies AI \cdot IF = SI \cdot II' = AI \cdot \frac {IF}{2} = \frac {SI}{2} \cdot II' = AI \cdot IM = EI \cdot IX \implies AEMX$ is cyclic.

Contact

Contact v_Enhance at https://www.facebook.com/v.Enhance.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_USAMO_Problems/Problem_3&oldid=178361"