Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AIME I Problems/Problem 13"

m
(→‎Solution 6 (Geometry))
Line 115: Line 115:
 
In <math>\triangle OFO_1 (OF = OO_1) OT</math> is bisector of <math>\angle O, OM</math> is median  
 
In <math>\triangle OFO_1 (OF = OO_1) OT</math> is bisector of <math>\angle O, OM</math> is median  
  
−
<math>\hspace{10mm} \implies O,T,</math>  and <math>M</math> are colinear.  
+
<math>\hspace{10mm} \implies O,T,</math>  and <math>M</math> are collinear.  
  
 
<cmath>\angle OCT = \angle ODT = \angle OET = 90^\circ \implies</cmath>
 
<cmath>\angle OCT = \angle ODT = \angle OET = 90^\circ \implies</cmath>
  
−
<math>OCTDE</math> is inscribed in <math>\Omega, OT</math> is diameter <math>\Omega.</math>  
+
<math>OCTDE</math> is cyclic (in <math>\Omega), OT</math> is diameter <math>\Omega.</math>  
 
<math>O_1O_2 \perp AB, OM \perp FO_1 \implies \angle FO_1O_2 = \angle OTE</math>
 
<math>O_1O_2 \perp AB, OM \perp FO_1 \implies \angle FO_1O_2 = \angle OTE</math>
 
<math>\angle OTE = \angle ODE</math> as they intercept the same arc  <math> \overset{\Large\frown}{OE}</math> in <math>\Omega.</math>
 
<math>\angle OTE = \angle ODE</math> as they intercept the same arc  <math> \overset{\Large\frown}{OE}</math> in <math>\Omega.</math>
Line 128: Line 128:
 
Since <math>r_{1}=625</math> and <math>r_{2}=961</math>, the answer is <math>2\cdot|961-625|=\boxed{672}</math>.
 
Since <math>r_{1}=625</math> and <math>r_{2}=961</math>, the answer is <math>2\cdot|961-625|=\boxed{672}</math>.
  
−
'''Shelomovskii, vvsss,  www.deoma-cmd.ru'''
+
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
==Video Solution==
 
==Video Solution==

Revision as of 02:09, 31 August 2022

Problem

Circles $\omega_1$ and $\omega_2$ with radii $961$ and $625$, respectively, intersect at distinct points $A$ and $B$. A third circle $\omega$ is externally tangent to both $\omega_1$ and $\omega_2$. Suppose line $AB$ intersects $\omega$ at two points $P$ and $Q$ such that the measure of minor arc $\widehat{PQ}$ is $120^{\circ}$. Find the distance between the centers of $\omega_1$ and $\omega_2$.

Solution 1 (Properties of Radical Axis)

Let $O_i$ and $r_i$ be the center and radius of $\omega_i$, and let $O$ and $r$ be the center and radius of $\omega$.

Since $\overline{AB}$ extends to an arc with arc $120^\circ$, the distance from $O$ to $\overline{AB}$ is $r/2$. Let $X=\overline{AB}\cap \overline{O_1O_2}$. Consider $\triangle OO_1O_2$. The line $\overline{AB}$ is perpendicular to $\overline{O_1O_2}$ and passes through $X$. Let $H$ be the foot from $O$ to $\overline{O_1O_2}$; so $HX=r/2$. We have by tangency $OO_1=r+r_1$ and $OO_2=r+r_2$. Let $O_1O_2=d$. [asy] unitsize(3cm); pointpen=black; pointfontpen=fontsize(9); pair A=dir(110), B=dir(230), C=dir(310); DPA(A--B--C--A); pair H = foot(A, B, C); draw(A--H); pair X = 0.3*B + 0.7*C; pair Y = A+X-H; draw(X--1.3*Y-0.3*X); draw(A--Y, dotted); pair R1 = 1.3*X-0.3*Y; pair R2 = 0.7*X+0.3*Y; draw(R1--X); D("O",A,dir(A)); D("O_1",B,dir(B)); D("O_2",C,dir(C)); D("H",H,dir(270)); D("X",X,dir(225)); D("A",R1,dir(180)); D("B",R2,dir(180)); draw(rightanglemark(Y,X,C,3)); [/asy] Since $X$ is on the radical axis of $\omega_1$ and $\omega_2$, it has equal power with respect to both circles, so \[O_1X^2 - r_1^2 = O_2X^2-r_2^2 \implies O_1X-O_2X = \frac{r_1^2-r_2^2}{d}\]since $O_1X+O_2X=d$. Now we can solve for $O_1X$ and $O_2X$, and in particular, \begin{align*} O_1H &= O_1X - HX = \frac{d+\frac{r_1^2-r_2^2}{d}}{2} - \frac{r}{2} \\ O_2H &= O_2X + HX = \frac{d-\frac{r_1^2-r_2^2}{d}}{2} + \frac{r}{2}. \end{align*} We want to solve for $d$. By the Pythagorean Theorem (twice): \begin{align*} &\qquad -OH^2 = O_2H^2 - (r+r_2)^2 = O_1H^2 - (r+r_1)^2 \\ &\implies \left(d+r-\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_2)^2 = \left(d-r+\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_1)^2 \\ &\implies 2dr - 2(r_1^2-r_2)^2-8rr_2-4r_2^2 = -2dr+2(r_1^2-r_2^2)-8rr_1-4r_1^2 \\ &\implies 4dr = 8rr_2-8rr_1 \\ &\implies d=2r_2-2r_1 \end{align*} Therefore, $d=2(r_2-r_1) = 2(961-625)=\boxed{672}$.

Solution 2 (Linearity)

Let $O_{1}$, $O_{2}$, and $O$ be the centers of $\omega_{1}$, $\omega_{2}$, and $\omega$ with $r_{1}$, $r_{2}$, and $r$ their radii, respectively. Then, the distance from $O$ to the radical axis $\ell\equiv\overline{AB}$ of $\omega_{1}, \omega_{2}$ is equal to $\frac{1}{2}r$. Let $x=O_{1}O_{2}$ and $O^{\prime}$ the orthogonal projection of $O$ onto line $\ell$. Define the function $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ by \[f(X)=\text{Pow}_{\omega_{1}}(X)-\text{Pow}_{\omega_{2}}(X).\] Then \begin{align*} f(O_{1})=-r_{1}^{2}-(x-r_{2})(x+r_{2})&=-x^{2}+r_{2}^{2}-r_{1}^{2}, \\ f(O_{2})=(x-r_{1})(x+r_{1})-(-r_{2}^{2})&=x^{2}+r_{2}^{2}-r_{1}^{2}, \\ f(O)=r(r+2r_{1})-r(r+2r_{2})&=2r(r_{1}-r_{2}), \\ f(O^{\prime})&=0. \end{align*} By Linearity of Power of a Point, \[\frac{f(O_{2})-f(O_{1})}{f(O)-f(O^{\prime})}=\frac{O_{1}O_{2}}{OO^{\prime}}=\frac{x}{\tfrac{1}{2}r}=\frac{2x}{r}.\] Notice that $f(O_{2})-f(O_{1})=x^{2}-(-x^{2})=2x^{2}$ and $f(O)-f(O^{\prime})=2r(r_{1}-r_{2})$, thus \begin{align*}\frac{2x^{2}}{2r(r_{1}-r_{2})}&=\frac{2x}{r}\end{align*} Dividing both sides by $\frac{2x}{r}$ (which is obviously nonzero as $x$ is nonzero) gives us \begin{align*}\frac{x}{2(r_{1}-r_{2})}&=1\end{align*} so $x=2(r_{1}-r_{2})$. Since $r_{1}=961$ and $r_{2}=625$, the answer is $x=2\cdot(961-625)=\boxed{672}$.

Solution 3

Denote by $O_1$, $O_2$, and $O$ the centers of $\omega_1$, $\omega_2$, and $\omega$, respectively. Let $R_1 = 961$ and $R_2 = 625$ denote the radii of $\omega_1$ and $\omega_2$ respectively, $r$ be the radius of $\omega$, and $\ell$ the distance from $O$ to the line $AB$. We claim that\[\dfrac{\ell}{r} = \dfrac{R_2-R_1}{d},\]where $d = O_1O_2$. This solves the problem, for then the $\widehat{PQ} = 120^\circ$ condition implies $\tfrac{\ell}r = \cos 60^\circ = \tfrac{1}{2}$, and then we can solve to get $d = \boxed{672}$. [asy] import olympiad; size(230pt); defaultpen(linewidth(0.8)+fontsize(10pt)); real r1 = 17, r2 = 27, d = 35, r = 18; pair O1 = origin, O2 = (d,0); path w1 = circle(origin,r1), w2 = circle((d,0),r2), w1p = circle(origin,r1+r), w2p = circle((d,0), r2 + r); pair[] X = intersectionpoints(w1,w2), Y = intersectionpoints(w1p,w2p); pair O = Y[1]; path w = circle(Y[1],r); pair Xp = 5 * X[1] - 4 * X[0]; pair[] P = intersectionpoints(Xp--X[0],w); label("$O_1$",origin,N); label("$O_2$",(d,0),N); label("$O$",Y[1],SW); draw(origin--Y[1]--(d,0)--cycle,gray(0.6)); pair T = foot(O,O1,O2), Tp = foot(O,X[0],X[1]); draw(Tp--O--T^^rightanglemark(O,T,O1,60)^^rightanglemark(O,Tp,X[0],60),gray(0.6)); draw(w^^w1^^w2^^P[0]--X[0]); dot(Y[1]^^origin^^(d,0)); label("$X$",T,N,gray(0.6)); label("$Y$",foot(X[0],O1,O2),NE,gray(0.6)); label("$\ell$",(O+Tp)/2,S,gray(0.6)); [/asy]

Denote by $O_1$ and $O_2$ the centers of $\omega_1$ and $\omega_2$ respectively. Set $X$ as the projection of $O$ onto $O_1O_2$, and denote by $Y$ the intersection of $AB$ with $O_1O_2$. Note that $\ell = XY$. Now recall that\[d(O_2Y-O_1Y) = O_2Y^2 - O_1Y^2 = R_2^2 - R_1^2.\]Furthermore, note that\begin{align*}d(O_2X - O_1X) &= O_2X^2 - O_1X^2= O_2O^2 - O_1O^2 \\ &= (R_2 + r)^2 - (R_1+r)^2 = (R_2^2 - R_1^2) + 2r(R_2 - R_1).\end{align*}Substituting the first equality into the second one and subtracting yields\[2r(R_2 - R_1) = d(O_2X - O_1X) - d(O_2Y - O_1Y) = 2dXY,\]which rearranges to the desired.

Solution 4 (Quick)

Suppose we label the points as shown here. By radical axis, the tangents to $\omega$ at $D$ and $E$ intersect on $AB$. Thus $PDQE$ is harmonic, so the tangents to $\omega$ at $P$ and $Q$ intersect at $X \in DE$. Moreover, $OX \parallel O_1O_2$ because both $OX$ and $O_1O_2$ are perpendicular to $AB$, and $OX = 2OP$ because $\angle POQ = 120^{\circ}$. Thus\[O_1O_2 = O_1Y - O_2Y = 2 \cdot 961 - 2\cdot 625 = \boxed{672}\]by similar triangles.

~mathman3880

Solution 5 (Official MAA)

Like in other solutions, let $O$ be the center of $\omega$ with $r$ its radius; also, let $O_{1}$ and $O_{2}$ be the centers of $\omega_{1}$ and $\omega_{2}$ with $R_{1}$ and $R_{2}$ their radii, respectively. Let line $OP$ intersect line $O_{1}O_{2}$ at $T$, and let $u=TO_{2}$, $v=TO_{1}$, $x=PT$, where the length $O_{1}O_{2}$ splits as $u+v$. Because the lines $PQ$ and $O_{1}O_{2}$ are perpendicular, lines $OT$ and $O_{1}O_{2}$ meet at a $60^{\circ}$ angle.

Applying the Law of Cosines to $\triangle O_{2}PT$, $\triangle O_{1}PT$, $\triangle O_{2}OT$, and $\triangle O_{1}OT$ gives \begin{align*}\triangle O_{2}PT&:O_{2}P^{2}=u^{2}+x^{2}-ux \\ \triangle O_{1}PT&:O_{1}P^{2}=v^{2}+x^{2}+vx \\ \triangle O_{2}OT&:(r+R_{2})^{2}=u^{2}+(r+x)^{2}-u(r+x) \\ \triangle O_{1}OT&:(r+R_{1})^{2}=v^{2}+(r+x)^{2}+v(r+x)\end{align*}

Adding the first and fourth equations, then subtracting the second and third equations gives us \[\left(O_{2}P^{2}-O_{1}P^{2}\right)+\left(R_{1}^{2}-R_{2}^{2}\right)+2r(R_{1}-R_{2})=r(u+v)\]

Since $P$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$, the power of point $P$ with respect to either circle is \[O_{2}P^{2}-R_{2}^{2}=O_{1}P^{2}-R_{1}^{2}.\]

Hence $2r(R_{1}-R_{2})=r(u+v)$ which simplifies to \[u+v=2(R_{1}-R_{2}).\]

The requested distance \[O_{1}O_{2}=O_{1}T+O_{2}T=u+v\] is therefore equal to $2\cdot(961-625)=\boxed{672}$.

Solution 6 (Geometry)

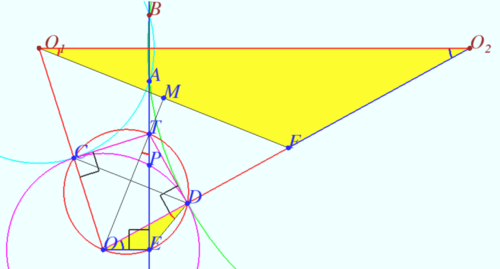
2021 AIME I 13.png

Let circle $\omega$ tangent circles $\omega_1$ and $\omega_2,$ respectively at distinct points $C$ and $D$. Let $O, O_1, O_2 (r, r_1, r_2)$ be the centers (the radii) of $\omega, \omega_1$ and $\omega_2,$ respectively. WLOG $r_1 < r_2.$ Let $F$ be the point of $OO_2$ such, that $OO_1 =OF.$ Let $M$ be the midpoint $FO_1, OE \perp AB, CT$ be the radical axes of $\omega_1$ and $\omega, T \in AB.$

Then $T$ is radical center of $\omega, \omega_1$ and $\omega_2, TD = CT.$

In $\triangle OFO_1 (OF = OO_1) OT$ is bisector of $\angle O, OM$ is median

$\hspace{10mm} \implies O,T,$ and $M$ are collinear.

\[\angle OCT = \angle ODT = \angle OET = 90^\circ \implies\]

$OCTDE$ is cyclic (in $\Omega), OT$ is diameter $\Omega.$ $O_1O_2 \perp AB, OM \perp FO_1 \implies \angle FO_1O_2 = \angle OTE$ $\angle OTE = \angle ODE$ as they intercept the same arc $\overset{\Large\frown}{OE}$ in $\Omega.$ \[OE \perp AB, O_1O_2 \perp AB \implies O_1 O_2 || OE \implies\] \[\angle OO_2O_1 = \angle O_2 OE \implies \triangle ODE \sim \triangle O_2 O_1 F \implies\] \[\frac {OE}{OD} = \frac {O_2F}{O_1O_2} \implies \cos \frac {120^\circ}{2} = \frac{r_2 + r - r_1 -r} {O_1O_2}\implies {O_1O_2}= 2|r_2 – r_1|.\]

Since $r_{1}=625$ and $r_{2}=961$, the answer is $2\cdot|961-625|=\boxed{672}$.

vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/gN7Ocu3D62M ~Math Problem Solving Skills


Video Solution

Who wanted to see animated video solutions can see this. I found this really helpful.

https://youtu.be/YtZ8_7i833E

P.S: This video is not made by me. And solution is same like below solutions.

≈@rounak138

See Also

2021 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 12 		Followed by
Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AIME_I_Problems/Problem_13&oldid=177744"