Difference between revisions of "Mock AIME 4 2006-2007 Problems/Problem 4"
(img, box, cat) |
|||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
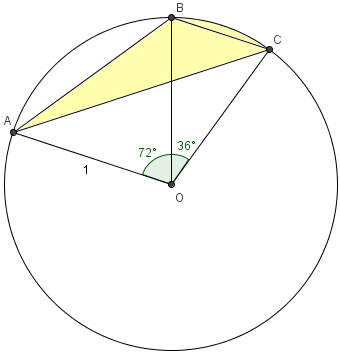
[[Point]]s <math>A</math>, <math>B</math>, and <math>C</math> are on the [[circumference]] of a unit [[circle]] so that the measure of <math>\widehat{AB}</math> is <math>72^{\circ}</math>, the measure of <math>\widehat{BC}</math> is <math>36^{\circ}</math>, and the measure of <math>\widehat{AC}</math> is <math>108^\circ</math>. The area of the triangular shape bounded by <math>\widehat{BC}</math> and [[line segment]]s <math>\overline{AB}</math> and <math>\overline{AC}</math> can be written in the form <math>\frac{m}{n} \cdot \pi</math>, where <math>m</math> and <math>n</math> are [[relatively prime]] [[positive integer]]s. Find <math>m + n</math>. | [[Point]]s <math>A</math>, <math>B</math>, and <math>C</math> are on the [[circumference]] of a unit [[circle]] so that the measure of <math>\widehat{AB}</math> is <math>72^{\circ}</math>, the measure of <math>\widehat{BC}</math> is <math>36^{\circ}</math>, and the measure of <math>\widehat{AC}</math> is <math>108^\circ</math>. The area of the triangular shape bounded by <math>\widehat{BC}</math> and [[line segment]]s <math>\overline{AB}</math> and <math>\overline{AC}</math> can be written in the form <math>\frac{m}{n} \cdot \pi</math>, where <math>m</math> and <math>n</math> are [[relatively prime]] [[positive integer]]s. Find <math>m + n</math>. | ||
| + | |||
==Solution== | ==Solution== | ||
| − | + | [[Image:2007_4_MockAIME-4.png]] | |
| + | |||
Let the center of the circle be <math>O</math>. The area of the desired region is easily seen to be that of sector <math>BOC</math> plus the area of triangle <math>AOB</math> minus the area of triangle <math>AOC</math>. Using the area formula <math>K_{\triangle XYZ} = \frac{1}{2} XY \cdot YZ \cdot \sin Y</math> to compute the areas of the two triangles, this is <math>\pi \cdot \frac{36}{360} + \frac{1}{2}\sin 72^\circ - \frac{1}{2}\sin108^{\circ} = \frac{1}{10}\cdot \pi</math>, so the answer is <math>1 + 10 = 011</math>. | Let the center of the circle be <math>O</math>. The area of the desired region is easily seen to be that of sector <math>BOC</math> plus the area of triangle <math>AOB</math> minus the area of triangle <math>AOC</math>. Using the area formula <math>K_{\triangle XYZ} = \frac{1}{2} XY \cdot YZ \cdot \sin Y</math> to compute the areas of the two triangles, this is <math>\pi \cdot \frac{36}{360} + \frac{1}{2}\sin 72^\circ - \frac{1}{2}\sin108^{\circ} = \frac{1}{10}\cdot \pi</math>, so the answer is <math>1 + 10 = 011</math>. | ||
| − | --- | + | ==See also== |
| + | {{Mock AIME box|year=2006-2007|n=4|num-b=3|num-a=5|source=125025}} | ||
| − | + | [[Category:Intermediate Geometry Problems]] | |
| − | |||
| − | |||
Latest revision as of 14:52, 8 October 2007
Problem
Points ![]() ,
, ![]() , and
, and ![]() are on the circumference of a unit circle so that the measure of
are on the circumference of a unit circle so that the measure of ![]() is
is ![]() , the measure of
, the measure of ![]() is
is ![]() , and the measure of
, and the measure of ![]() is
is ![]() . The area of the triangular shape bounded by
. The area of the triangular shape bounded by ![]() and line segments
and line segments ![]() and
and ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution
Let the center of the circle be ![]() . The area of the desired region is easily seen to be that of sector
. The area of the desired region is easily seen to be that of sector ![]() plus the area of triangle
plus the area of triangle ![]() minus the area of triangle
minus the area of triangle ![]() . Using the area formula
. Using the area formula ![]() to compute the areas of the two triangles, this is
to compute the areas of the two triangles, this is ![]() , so the answer is
, so the answer is ![]() .
.
See also
| Mock AIME 4 2006-2007 (Problems, Source) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||