Difference between revisions of "2016 AIME II Problems/Problem 10"
(→Solution 5 (5 = 2 + 3)) |
(→Solution 5 (5 = 2 + 3)) |
||
| Line 78: | Line 78: | ||
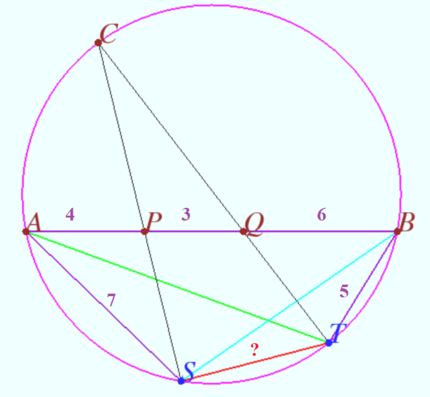
==Solution 5 (5 = 2 + 3)== | ==Solution 5 (5 = 2 + 3)== | ||
| − | [[File:2016 AIME II 10.png| | + | [[File:2016 AIME II 10.png|430px|right]] |
By Ptolemy's Theorem applied to quadrilateral <math>ASTB</math>, we find | By Ptolemy's Theorem applied to quadrilateral <math>ASTB</math>, we find | ||
<cmath>AS\cdot BT+AB\cdot ST=AT\cdot BS.</cmath> | <cmath>AS\cdot BT+AB\cdot ST=AT\cdot BS.</cmath> | ||
Revision as of 01:39, 23 June 2022
Contents
Problem
Triangle ![]() is inscribed in circle
is inscribed in circle ![]() . Points
. Points ![]() and
and ![]() are on side
are on side ![]() with
with ![]() . Rays
. Rays ![]() and
and ![]() meet
meet ![]() again at
again at ![]() and
and ![]() (other than
(other than ![]() ), respectively. If
), respectively. If ![]() and
and ![]() , then
, then ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
![[asy] import cse5; pathpen = black; pointpen = black; pointfontsize = 9; size(8cm); pair A = origin, B = (13,0), P = (4,0), Q = (7,0), T = B + 5 dir(220), C = IP(circumcircle(A,B,T),Line(T,Q,-0.1,10)), S = IP(circumcircle(A,B,C),Line(C,P,-0.1,10)); Drawing(A--B--C--cycle); D(circumcircle(A,B,C),rgb(0,0.6,1)); DrawPathArray(C--S^^C--T,rgb(1,0.4,0.1)); DrawPathArray(A--S^^B--T,rgb(0,0.4,0)); D(S--T,rgb(1,0.2,0.4)); D("A",A,dir(215)); D("B",B,dir(330)); D("P",P,dir(240)); D("Q",Q,dir(240)); D("T",T,dir(290)); D("C",C,dir(120)); D("S",S,dir(250)); MP("4",(A+P)/2,dir(90)); MP("3",(P+Q)/2,dir(90)); MP("6",(Q+B)/2,dir(90)); MP("5",(B+T)/2,dir(140)); MP("7",(A+S)/2,dir(40)); [/asy]](http://latex.artofproblemsolving.com/f/6/0/f603df291461fa6afd0563d94abdc2644aeb97ec.png) Let
Let ![]() ,
, ![]() , and
, and ![]() . Note that since
. Note that since ![]() we have
we have ![]() , so by the Ratio Lemma
, so by the Ratio Lemma ![]() Similarly, we can deduce
Similarly, we can deduce ![]() and hence
and hence ![]() .
.
Now Law of Sines on ![]() ,
, ![]() , and
, and ![]() yields
yields ![]() Hence
Hence ![]() so
so ![]() Hence
Hence ![]() and the requested answer is
and the requested answer is ![]() .
.
Edit: Note that the finish is much simpler. Once you get ![]() , you can solve quickly from there getting
, you can solve quickly from there getting ![]() .
.
Solution 2 (Projective Geometry)
Projecting through ![]() we have
we have ![]() which easily gives
which easily gives ![]()
Solution 3
By Ptolemy's Theorem applied to quadrilateral ![]() , we find
, we find
![]() Therefore, in order to find
Therefore, in order to find ![]() , it suffices to find
, it suffices to find ![]() . We do this using similar triangles, which can be found by using Power of a Point theorem.
. We do this using similar triangles, which can be found by using Power of a Point theorem.
As ![]() , we find
, we find
![]() Therefore,
Therefore, ![]() .
.
As ![]() , we find
, we find
![]() Therefore,
Therefore, ![]() .
.
As ![]() , we find
, we find
![]() Therefore,
Therefore, ![]() .
.
As ![]() , we find
, we find
![]() Therefore,
Therefore, ![]() . Thus we find
. Thus we find
![]() But now we can substitute in our previously found values for
But now we can substitute in our previously found values for ![]() and
and ![]() , finding
, finding
![]() Substituting this into our original expression from Ptolemy's Theorem, we find
Substituting this into our original expression from Ptolemy's Theorem, we find
 Thus the answer is
Thus the answer is ![]() .
.
Solution 4
Extend ![]() past
past ![]() to point
to point ![]() so that
so that ![]() is cyclic. Then, by Power of a Point on
is cyclic. Then, by Power of a Point on ![]() ,
, ![]() . By Power of a Point on
. By Power of a Point on ![]() ,
, ![]() . Thus,
. Thus, ![]() , so
, so ![]() .
.
By the Inscribed Angle Theorem on ![]() ,
, ![]() . By the Inscribed Angle Theorem on
. By the Inscribed Angle Theorem on ![]() ,
, ![]() , so
, so ![]() . Since
. Since ![]() is cyclic,
is cyclic, ![]() . Thus,
. Thus, ![]() , so
, so ![]() . Solving for
. Solving for ![]() yields
yields ![]() , for a final answer of
, for a final answer of ![]() .
.
~ Leo.Euler
Solution 5 (5 = 2 + 3)
By Ptolemy's Theorem applied to quadrilateral ![]() , we find
, we find
![]() Projecting through
Projecting through ![]() we have
we have
![]() Therefore
Therefore ![]()
![]()
![]()
![]()
Shelomovskii, vvsss, www.deoma-cmd.ru
See also
| 2016 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.