Difference between revisions of "Stewart's theorem"
(→Proof 2 (Pythagorean Theorem)) |
(→Proof 2 (Pythagorean Theorem)) |
||
| Line 36: | Line 36: | ||
<cmath>amn = n(x+y+n)(x+y) = x^2n+2xyn+xn^2+y^2n+n^2y \text{ and}</cmath> | <cmath>amn = n(x+y+n)(x+y) = x^2n+2xyn+xn^2+y^2n+n^2y \text{ and}</cmath> | ||
| − | <cmath>d^ | + | <cmath>d^2a = (h^2+y^2)(x+y+n) = h^2x+h^2y+h^2n+y^2x+y^3+y^2n.</cmath> |
Notice that | Notice that | ||
Revision as of 15:32, 10 March 2022
Contents
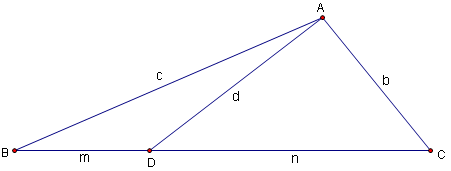
Statement
Given a triangle ![]() with sides of length
with sides of length ![]() opposite vertices are
opposite vertices are ![]() ,
, ![]() ,
, ![]() , respectively. If cevian
, respectively. If cevian ![]() is drawn so that
is drawn so that ![]() ,
, ![]() and
and ![]() , we have that
, we have that ![]() . (This is also often written
. (This is also often written ![]() , a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
, a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
Proof 1
Applying the Law of Cosines in triangle ![]() at angle
at angle ![]() and in triangle
and in triangle ![]() at angle
at angle ![]() , we get the equations
, we get the equations
Because angles ![]() and
and ![]() are supplementary,
are supplementary, ![]() . We can therefore solve both equations for the cosine term. Using the trigonometric identity
. We can therefore solve both equations for the cosine term. Using the trigonometric identity ![]() gives us
gives us
Setting the two left-hand sides equal and clearing denominators, we arrive at the equation: ![]() .
However,
.
However,
![]() so
so
![]() and
and
![]() This simplifies our equation to yield
This simplifies our equation to yield ![]() or Stewart's theorem.
or Stewart's theorem.
Proof 2 (Pythagorean Theorem)
Let the altitude from ![]() to
to ![]() meet
meet ![]() at
at ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . So, applying Pythagorean Theorem on
. So, applying Pythagorean Theorem on ![]() yields
yields
![]()
Since ![]() ,
, ![]()
Applying Pythagorean on ![]() yields
yields
![]()
Substituting ![]() ,
, ![]() , and
, and ![]() in
in ![]() and
and ![]() gives
gives
![]()
![]()
Notice that
![]()
![]() are equal to each other. Thus,
are equal to each other. Thus, ![]() Rearranging the equation gives Stewart's Theorem:
Rearranging the equation gives Stewart's Theorem:
![]()
~sml1809
Nearly Identical Video Proof with an Example by TheBeautyofMath
~IceMatrix









