Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1987 AIME Problems/Problem 15"
(→‎Solution)
 
Line 9: Line 9:
 
Because all the [[triangle]]s in the figure are [[similar]] to triangle <math>ABC</math>, it's a good idea to use [[area ratios]]. In the diagram above, <math>\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.</math> Hence, <math>T_3 = \frac {440}{441}T_1</math> and <math>T_4 = \frac {440}{441}T_2</math>. Additionally, the area of triangle <math>ABC</math> is equal to both <math>T_1 + T_2 + 441</math> and <math>T_3 + T_4 + T_5 + 440.</math>  
 
Because all the [[triangle]]s in the figure are [[similar]] to triangle <math>ABC</math>, it's a good idea to use [[area ratios]]. In the diagram above, <math>\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.</math> Hence, <math>T_3 = \frac {440}{441}T_1</math> and <math>T_4 = \frac {440}{441}T_2</math>. Additionally, the area of triangle <math>ABC</math> is equal to both <math>T_1 + T_2 + 441</math> and <math>T_3 + T_4 + T_5 + 440.</math>  
  
−
Setting the equations equal and solving for <math>T_5</math>, <math>T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}</math>. Therefore, <math>441T_5 = 441 + T_1 + T_2</math>. However, <math>441 + T_1 + T_2</math> is equal to the area of triangle <math>ABC</math>! This means that the ratio between the areas <math>T_5</math> and <math>ABC</math> is <math>441</math>, and the ratio between the sides is <math>\sqrt {441} = 21</math>. As a result, <math>AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}</math>. We now need <math>(AC)(BC)</math> to find the value of <math>AC + BC</math>, because <math>AB^2 + BC^2 + 2(AC)(BC) = (AC + BC)^2</math>.
+
Setting the equations equal and solving for <math>T_5</math>, <math>T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}</math>. Therefore, <math>441T_5 = 441 + T_1 + T_2</math>. However, <math>441 + T_1 + T_2</math> is equal to the area of triangle <math>ABC</math>! This means that the ratio between the areas <math>T_5</math> and <math>ABC</math> is <math>441</math>, and the ratio between the sides is <math>\sqrt {441} = 21</math>. As a result, <math>AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}</math>. We now need <math>(AC)(BC)</math> to find the value of <math>AC + BC</math>, because <math>AC^2 + BC^2 + 2(AC)(BC) = (AC + BC)^2</math>.
  
 
Let <math>h</math> denote the height to the [[hypotenuse]] of triangle <math>ABC</math>. Notice that <math>h - \frac {1}{21}h = \sqrt {440}</math>. (The height of <math>ABC</math> decreased by the corresponding height of <math>T_5</math>) Thus, <math>(AB)(h) = (AC)(BC) = 22\cdot 21^2</math>. Because <math>AC^2 + BC^2 +  2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2</math>, <math>AC + BC = (21)(22) = \boxed{462}</math>.
 
Let <math>h</math> denote the height to the [[hypotenuse]] of triangle <math>ABC</math>. Notice that <math>h - \frac {1}{21}h = \sqrt {440}</math>. (The height of <math>ABC</math> decreased by the corresponding height of <math>T_5</math>) Thus, <math>(AB)(h) = (AC)(BC) = 22\cdot 21^2</math>. Because <math>AC^2 + BC^2 +  2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2</math>, <math>AC + BC = (21)(22) = \boxed{462}</math>.

Latest revision as of 17:05, 19 February 2022

Problem

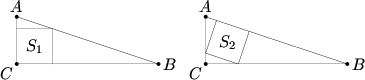
Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$, as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$.

AIME 1987 Problem 15.png

Solution

1987 AIME-15a.png

Because all the triangles in the figure are similar to triangle $ABC$, it's a good idea to use area ratios. In the diagram above, $\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.$ Hence, $T_3 = \frac {440}{441}T_1$ and $T_4 = \frac {440}{441}T_2$. Additionally, the area of triangle $ABC$ is equal to both $T_1 + T_2 + 441$ and $T_3 + T_4 + T_5 + 440.$

Setting the equations equal and solving for $T_5$, $T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}$. Therefore, $441T_5 = 441 + T_1 + T_2$. However, $441 + T_1 + T_2$ is equal to the area of triangle $ABC$! This means that the ratio between the areas $T_5$ and $ABC$ is $441$, and the ratio between the sides is $\sqrt {441} = 21$. As a result, $AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}$. We now need $(AC)(BC)$ to find the value of $AC + BC$, because $AC^2 + BC^2 + 2(AC)(BC) = (AC + BC)^2$.

Let $h$ denote the height to the hypotenuse of triangle $ABC$. Notice that $h - \frac {1}{21}h = \sqrt {440}$. (The height of $ABC$ decreased by the corresponding height of $T_5$) Thus, $(AB)(h) = (AC)(BC) = 22\cdot 21^2$. Because $AC^2 + BC^2 + 2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2$, $AC + BC = (21)(22) = \boxed{462}$.

Easy Trig Solution

Let $\tan\angle ABC = x$. Now using the 1st square, $AC=21(1+x)$ and $CB=21(1+x^{-1})$. Using the second square, $AB=\sqrt{440}(1+x+x^{-1})$. We have $AC^2+CB^2=AB^2$, or \[441(x^2+x^{-2}+2x+2x^{-1}+2)=440(x^2+x^{-2}+2x+2x^{-1}+3).\] Rearranging and letting $u=x+x^{-1} \Rightarrow u^2 - 2 = x^2 + x^{-2}$ gives us $u^2+2u-440=0.$ We take the positive root, so $u=20$, which means $AC+CB=21(2+x+x^{-1})=21(2+u)=\boxed{462}$.

Messy Trig Solution

Let $\theta$ be the smaller angle in the triangle. Then the sum of shorter and longer leg is $\sqrt{441}(2+\tan{\theta}+\cot{\theta})$. We observe that the short leg has length $\sqrt{441}(1+\tan{\theta}) = \sqrt{440}(\sec{\theta}+\sin{\theta})$. Grouping and squaring, we get $\sqrt{\frac{440}{441}} = \frac{\sin{\theta}+\cos{\theta}}{1+\sin{\theta}\cos{\theta}}$. Squaring and using the double angle identity for sine, we get, $110(\sin{2\theta})^2 + \sin{2\theta} - 1 = 0$. Solving, we get $\sin{2\theta} = \frac{1}{10}$. Now to find $\tan{\theta}$, we find $\cos{2\theta}$ using the Pythagorean Identity, and then use the tangent double angle identity. Thus, $\tan{\theta} = 10-3\sqrt{11}$. Substituting into the original sum, we get $\boxed{462}$.

Solution 4 (Algebra)

[asy] size(200); pair A, B, C, D, E, F; A = (0, 5); B = (12, 0); C = (0, 0); D = (0, 60/17); E = (60/17, 60/17); F = (60/17, 0); draw(A--B--C--cycle); draw(D--E--F); label("$A$",A,N); label("$B$",B,dir(0)); label("$C$",C,SW); label("$D$",D,W); label("$E$",E,NE); label("$F$",F,S); label("$S_1$",(30/17,30/17)); [/asy]

[asy] size(200); pair A, B, C, W, X, Y, Z; A = (0, 5); B = (12, 0); C = (0, 0); real m = 1.31004366812; real n = 3.1441048035; W = (0,m); X = (m,m+n); Y = (m+n,n); Z = (n,0); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle); label("$A$",A,N); label("$B$",B,dir(0)); label("$C$",C,SW); label("$W$",W,dir(180)); label("$X$",X,NE); label("$Y$",Y,NE); label("$Z$",Z,S); label("$S_2$",(2.22707423581,2.22707423581)); [/asy]

Label points as above. Let $x=AC$, $y=BC$, $s_1 = 21$ be the side length of $S_1$, and $s_2 = \sqrt{440}$ be the side length of $S_2$.

Since $\triangle ABC\sim\triangle AED$, we have $\frac{x}{y} = \frac{x-s_1}{s_1}$

$\implies xs_1=xy-ys_1$

$\implies xy=s_1(x+y)$

$\implies xy=21(x+y) \qquad \qquad (*)$.

Since $\triangle ABC\sim\triangle AWX\sim\triangle ZBY$, we have $s_2 + \frac{s_2x}{y} + \frac{s_2y}{x}=\sqrt{x^2+y^2}$

$\implies s_2(x^2+xy+y^2)=xy\sqrt{x^2+y^2}$

$\implies s_2^2(x^2+xy+y^2)^2 = x^2y^2(x^2+y^2)$

$\implies 440(x^2+xy+y^2)^2 = x^2y^2(x^2+y^2)$

Let $t=x+y$. Repeatedly applying $(*)$, we get \[440(t^2-21t)^2 = 441t^2(t^2 - 42t)\] \[440(t-21)^2 = 441(t^2-42t)\] \[440t^2 - 42\cdot 440t + 440\cdot 441 = 441t^2 - 441\cdot 42t\] \[t^2-42t-440\cdot 441=0\] \[(t-21)^2 = 441^2\] \[t-21=441\] \[t=\boxed{462}\]

~rayfish

See also

1987 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last
Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1987_AIME_Problems/Problem_15&oldid=171601"