Difference between revisions of "2006 AIME A Problems/Problem 1"
I_like_pie (talk | contribs) |
(→Problem) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | In | + | In quadrilateral <math> ABCD , \angle B </math> is a right angle, diagonal <math> \overline{AC} </math> is perpendicular to <math> \overline{CD}, AB=18, BC=21, </math> and <math> CD=14. </math> Find the perimeter of <math> ABCD. </math> |
== Solution == | == Solution == | ||
Revision as of 12:53, 25 September 2007
Problem
In quadrilateral ![]() is a right angle, diagonal
is a right angle, diagonal ![]() is perpendicular to
is perpendicular to ![]() and
and ![]() Find the perimeter of
Find the perimeter of ![]()
Solution
Let the side length be called ![]() .
.
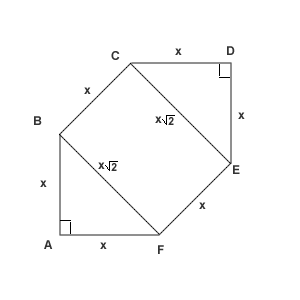
Then ![]() .
.
The diagonal ![]() .
.
Then the areas of the triangles AFB and CDE in total are ![]() ,
and the area of the rectangle BCEF equals
,
and the area of the rectangle BCEF equals ![]()
Then we have to solve the equation
![]() .
.
![]()
![]()
![]()
Therefore, AB is 46.









