Difference between revisions of "Parabola"
(→Graphing Parabolas) |
(→Graphing Parabolas) |
||
| Line 10: | Line 10: | ||
==Graphing Parabolas== | ==Graphing Parabolas== | ||
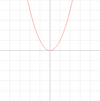
| − | [[Image:Parabola.png|thumb|right| | + | [[Image:Parabola.png|thumb|right|100px|100px|The graph of <math>y=x^2</math>]] |
Using the completed square form, <math>y - k = a(x - h)^2</math> or <math>x - h = a(y - k)^2</math>, the vertex of the graph is at the point <math>(h, k)</math>. The graph appears vertically if the <math>x</math> term is squared, and horizontal if the <math>y</math> term is squared. The graph will be oriented (opens up) upwards/right if <math>a</math> is positive, and will be downwards/left if <math>a</math> is negative. | Using the completed square form, <math>y - k = a(x - h)^2</math> or <math>x - h = a(y - k)^2</math>, the vertex of the graph is at the point <math>(h, k)</math>. The graph appears vertically if the <math>x</math> term is squared, and horizontal if the <math>y</math> term is squared. The graph will be oriented (opens up) upwards/right if <math>a</math> is positive, and will be downwards/left if <math>a</math> is negative. | ||
Revision as of 19:13, 14 September 2007
A parabola is a type of conic section. A parabola is a locus of points that are equidistant from a point (the focus) and a line (the directrix).
Contents
Parabola Equations
There are several "standard" ways to write the equation of a parabola. The first is polynomial form: 
where a, b, and c are constants. This is useful for manipulating the polynomial.
The second is completed square form, or 
where a, h, and k are constants and the vertex is (h,k). This is very useful for graphing the quadratic because the vertex and stretching factor are immediately before you.
The third way is the conic section form, or 
or 
where the p is a constant, and is the distance from the focus to the vertex.
Graphing Parabolas
Using the completed square form, 
or 
, the vertex of the graph is at the point 
. The graph appears vertically if the 
term is squared, and horizontal if the 
term is squared. The graph will be oriented (opens up) upwards/right if 
is positive, and will be downwards/left if is negative.
Problems
Introductory
- A parabola with equation
passes through the points (2,3) and (4,3). What is 
?
passes through the points (2,3) and (4,3). What is 
?
Intermediate
Olympiad
See also
This article is a stub. Help us out by expanding it.
