Difference between revisions of "Jadhav Angular Formula"

Revision as of 22:13, 25 August 2021

Jadhav Angular Formula evaluates the angle between any two sides of any triangle given length of all the sides, invented by Indian mathematical scholar Jyotiraditya Jadhav.

Visual use

Jadhav Angular Formula

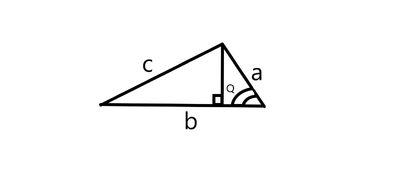
Let the angle angle between side length a and b be Q

Now as per the equation angle Q will be:

$\measuredangle Q = \arccos [a^2+b^2-c^2/2ab]$

Applications

Astrophysics: For finding angles between the vector of celestial bodies.

Aerodynamics: In finding the glide angle, angle of climb and various angles of attack.

Navigation: In finding real time locations.

Geography: In calculating distances between geographical locations.
Geometry: In finding angles between the two sides of any triangle.

Robotics: In operating arms and for studying robotic movements through vectors.
Teleportation and Quantum Physics: In studying oscillating motions of particles.

Trigonometric Cosine function

Now as in the figure of "Trigonometric Circle" as the angle theta increases and the transition line goes beyond 1st quadrant, the value of some trigonometric functions change from positive to negative, like cosine function the ratio will be negative in the second and 3rd quadrant, the angle is always calculated from positive x-axis. So in-case cosine function inverse of the $a^2+b^2-c^2 /(2ab)$ is a negative value then the angle which gives exactly same ratio in positive will be considered and subtracted from $\measuredangle$ 180 or $\pi$ radians (while dealing with radians) to get exact angle from x-axis.

The generalized formula where the ratio would be (-x), then exact angle can be found like this:

$\arccos (-x) =180 -\arccos (x)$ (while using degrees)

$\arccos (-x) =\pi-\arccos (x)$ (while using radians)

Other inventions by Jyotiraditya Jadhav

Read more about Jyotiraditya Jadhav here.

@@ Line 1: / Line 1: @@
 '''Jadhav Angular Formula''' evaluates the '''angle between any two sides''' of any triangle given length of all the sides, invented by Indian mathematical scholar '''[[Jyotiraditya Jadhav|Jyotiraditya Jadhav.]]'''
-== Introduction ==
-In any triangle given sides a,b and c , with '''longest side c''' the '''angle between the sides a and b''' can be found by:
-<math>\measuredangle = \cos^-1 [{a^2+b^2-c^2}(2ab)^-1] </math>
-==== Nomenclature: ====
-* '''Cosine function :''' The cosine function is one of the basic functions encountered in trigonometry (the others being the cosecant , cotangent, secant, sine , and tangent ). Let be an angle measured counterclockwise from the x -axis along the arc of the unit circle . Then is the horizontal coordinate of the arc endpoint.
-* <math>a^2  </math>: square of length of one side among the angle
-* <math>b^2 </math>: square of length of other side among the angle
-* <math>c^2 </math> : square of length of the longest side/ opposite side to the angle
 == Visual use ==

Page

Toolbox

Search