Difference between revisions of "2007 AMC 12A Problems/Problem 8"
(Fine, leave me to draw the diagram and an incorrect answer ;)) |
|||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | A star-polygon is drawn on a clock face by drawing a chord from each number to the fifth number counted clockwise from that number. That is, chords are drawn from 12 to 5, from 5 to 10, from 10 to 3, and so on, ending back at 12. What is the degree measure of the angle at each vertex in the star polygon? | + | A star-[[polygon]] is drawn on a clock face by drawing a [[chord]] from each number to the fifth number counted clockwise from that number. That is, chords are drawn from 12 to 5, from 5 to 10, from 10 to 3, and so on, ending back at 12. What is the degree measure of the [[angle]] at each [[vertex]] in the star polygon? |
| + | |||
| + | <math>\mathrm{(A)}\ 20\qquad \mathrm{(B)}\ 24\qquad \mathrm{(C)}\ 30\qquad \mathrm{(D)}\ 36\qquad \mathrm{(E)}\ 60</math> | ||
==Solution== | ==Solution== | ||
| − | + | [[Image:2007_AMC12A-8.png]] | |
| − | + | ||
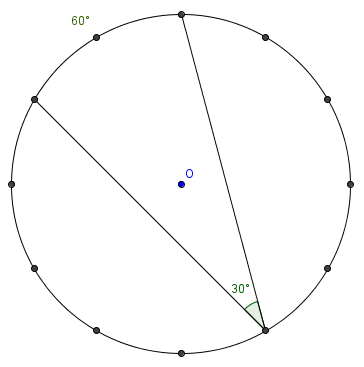
| + | We look at the angle between 12, 5, and 10. It subtends <math>\displaystyle \frac 16</math> of the circle, or <math>60</math> degrees (or you can see that the [[arc]] is <math>\frac 23</math> of the [[right angle]]). Thus, the angle at each vertex is an [[inscribed angle]] subtending <math>60</math> degrees, making the answer <math>\frac 1260 = 30^{\circ} \Longrightarrow \mathrm{(C)}</math> | ||
==See also== | ==See also== | ||
| − | + | {{AMC12 box|year=2007|ab=A|num-b=7|num-a=9}} | |
| − | + | ||
| − | + | [[Category:Introductory Geometry Problems]] | |
Revision as of 14:32, 9 September 2007
Problem
A star-polygon is drawn on a clock face by drawing a chord from each number to the fifth number counted clockwise from that number. That is, chords are drawn from 12 to 5, from 5 to 10, from 10 to 3, and so on, ending back at 12. What is the degree measure of the angle at each vertex in the star polygon?
Solution
We look at the angle between 12, 5, and 10. It subtends 
of the circle, or 
degrees (or you can see that the arc is 
of the right angle). Thus, the angle at each vertex is an inscribed angle subtending degrees, making the answer 
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 7 |
Followed by Problem 9 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
