Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1989 AIME Problems/Problem 12"
m (→‎Problem: Centered the image.)
Line 2: Line 2:
 
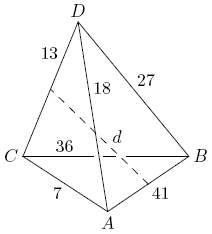
Let <math>ABCD</math> be a [[tetrahedron]] with <math>AB=41</math>, <math>AC=7</math>, <math>AD=18</math>, <math>BC=36</math>, <math>BD=27</math>, and <math>CD=13</math>, as shown in the figure. Let <math>d</math> be the distance between the [[midpoint]]s of [[edge]]s <math>AB</math> and <math>CD</math>. Find <math>d^{2}</math>.
 
Let <math>ABCD</math> be a [[tetrahedron]] with <math>AB=41</math>, <math>AC=7</math>, <math>AD=18</math>, <math>BC=36</math>, <math>BD=27</math>, and <math>CD=13</math>, as shown in the figure. Let <math>d</math> be the distance between the [[midpoint]]s of [[edge]]s <math>AB</math> and <math>CD</math>. Find <math>d^{2}</math>.
  
−
[[Image:AIME_1989_Problem_12.png]]
+
[[Image:AIME_1989_Problem_12.png|center]]
  
 
== Solution ==
 
== Solution ==

Revision as of 06:41, 7 August 2021

Problem

Let $ABCD$ be a tetrahedron with $AB=41$, $AC=7$, $AD=18$, $BC=36$, $BD=27$, and $CD=13$, as shown in the figure. Let $d$ be the distance between the midpoints of edges $AB$ and $CD$. Find $d^{2}$.

AIME 1989 Problem 12.png

Solution

Call the midpoint of $\overline{AB}$ $M$ and the midpoint of $\overline{CD}$ $N$. $d$ is the median of triangle $\triangle CDM$. The formula for the length of a median is $m=\sqrt{\frac{2a^2+2b^2-c^2}{4}}$, where $a$, $b$, and $c$ are the side lengths of triangle, and $c$ is the side that is bisected by median $m$. The formula is a direct result of the Law of Cosines applied twice with the angles formed by the median (Stewart's Theorem). We can also get this formula from the parallelogram law, that the sum of the squares of the diagonals is equal to the squares of the sides of a parallelogram (https://en.wikipedia.org/wiki/Parallelogram_law).

We first find $CM$, which is the median of $\triangle CAB$.

\[CM=\sqrt{\frac{98+2592-1681}{4}}=\frac{\sqrt{1009}}{2}\]

Now we must find $DM$, which is the median of $\triangle DAB$.

\[DM=\frac{\sqrt{425}}{2}\]

Now that we know the sides of $\triangle CDM$, we proceed to find the length of $d$.

\[d=\frac{\sqrt{548}}{2} \Longrightarrow d^2=\frac{548}{4}=\boxed{137}\]

See also

1989 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1989_AIME_Problems/Problem_12&oldid=159715"