Difference between revisions of "2021 JMPSC Sprint Problems/Problem 7"
(→Solution) |
(→Solution 2 (kind of adds on to solution 1)) |
||
| Line 10: | Line 10: | ||
==Solution 2 (kind of adds on to solution 1)== | ==Solution 2 (kind of adds on to solution 1)== | ||
| − | Since there are 2 ways to place 3 circles in a row in 4 circles, and 1 way to put three circles in a row in a row of three circles. There are 3 ways for each side of the equilateral triangle. Therefore, <math>3</math> * <math>(2+1)</math> = <math>\boxed{9}</math> ways total. | + | Since there are 2 ways to place 3 circles in a row in a row of 4 circles, and 1 way to put three circles in a row in a row of three circles. There are 3 ways for each side of the equilateral triangle. Therefore, <math>3</math> * <math>(2+1)</math> = <math>\boxed{9}</math> ways total. |
-Chenz1 (aka doge 34) | -Chenz1 (aka doge 34) | ||
Latest revision as of 09:53, 16 July 2021
Problem
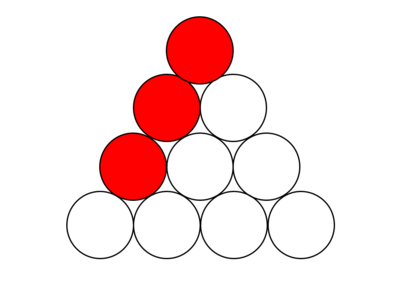
How many sets of three circles are in the diagram below such that their centers lie on the same line and each circle in the set is adjacent to another circle in the set? (Assume that if the centers of three circles appear to be on the same line, then they are on the same line. For example, the three red shaded circles count as one such set.)
Solution
Consider the equilateral triangle that the circles make. There are 
ways to pick the circles so that the row they make is parallel to each side of the equilateral triangle. Thus, there are 
ways total. [diagram needed]
~tigerzhang
Solution 2 (kind of adds on to solution 1)
Since there are 2 ways to place 3 circles in a row in a row of 4 circles, and 1 way to put three circles in a row in a row of three circles. There are 3 ways for each side of the equilateral triangle. Therefore, * 
= ways total.
-Chenz1 (aka doge 34)
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. 
