Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 JMPSC Sprint Problems/Problem 16"

(→‎Problem)
m (→‎Solution)
Line 6: Line 6:
  
 
==Solution==
 
==Solution==
 +
 +
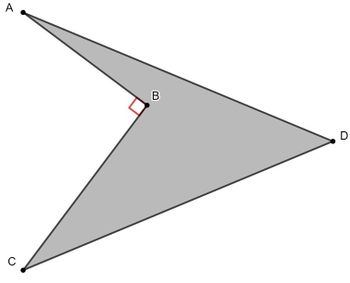
Notice that <math>[ABCD] = [ADC] - [ABC]</math> and <math>AC = \sqrt{12^2 + 16^2} = 20</math> by the Pythagorean Thereom. We then have that the area of triangle of <math>ADC</math> is <math>\frac{20 \cdot \sqrt{26^2 - 10^2}}{2} = 240</math>, and the area of triangle <math>ABC</math> is <math>\frac{12 \cdot 16}{2} = 96</math>, so the area of quadrilateral <math>ABCD</math> is <math>240 - 96 = 144</math>.
 +
 +
~Mathdreams

Revision as of 10:58, 11 July 2021

Problem

$ABCD$ is a concave quadrilateral with $AB = 12$, $BC = 16$, $AD = CD = 26$, and $\angle ABC=90^\circ$. Find the area of $ABCD$.

Sprint16.jpg

Solution

Notice that $[ABCD] = [ADC] - [ABC]$ and $AC = \sqrt{12^2 + 16^2} = 20$ by the Pythagorean Thereom. We then have that the area of triangle of $ADC$ is $\frac{20 \cdot \sqrt{26^2 - 10^2}}{2} = 240$, and the area of triangle $ABC$ is $\frac{12 \cdot 16}{2} = 96$, so the area of quadrilateral $ABCD$ is $240 - 96 = 144$.

~Mathdreams

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_JMPSC_Sprint_Problems/Problem_16&oldid=157851"