Difference between revisions of "2007 Cyprus MO/Lyceum/Problems"
I_like_pie (talk | contribs) m (→Problem 23) |
I_like_pie (talk | contribs) m (→Problem 27) |
||
| Line 424: | Line 424: | ||
</div> | </div> | ||
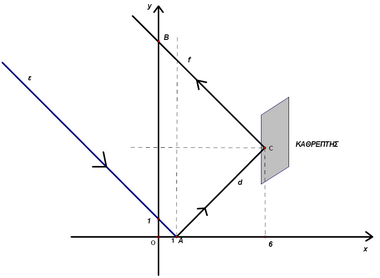
| − | In the following diagram the light beam <math>\epsilon</math> is reflected on the x-axis and the beam <math>d</math> , being reflected on a mirror parallel to the y-axis at distance 6, intersects the y-axis at point <math>B</math>. <br> | + | In the following diagram, the light beam <math>\epsilon</math> is reflected on the <math>x</math>-axis and the beam <math>d</math>, being reflected on a mirror parallel to the <math>y</math>-axis at distance 6, intersects the <math>y</math>-axis at point <math>B</math>. <br> |
The equation of line <math>f</math> is given by | The equation of line <math>f</math> is given by | ||
| − | Α. x+y-11=0 | + | Α. <math>x+y-11=0</math> |
| − | Β. x+y+11=0 | + | Β. <math>x+y+11=0</math> |
| − | C. x-y+11=0 | + | C. <math>x-y+11=0</math> |
| − | D. x-y-11=0 | + | D. <math>x-y-11=0</math> |
| − | Ε. y=-x+10 | + | Ε. <math>y=-x+10</math> |
[[2007 Cyprus MO/Lyceum/Problem 27|Solution]] | [[2007 Cyprus MO/Lyceum/Problem 27|Solution]] | ||
Revision as of 01:37, 7 June 2007
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 Problem 26
- 27 Problem 27
- 28 Problem 28
- 29 Problem 29
- 30 Problem 30
- 31 See also
Problem 1
If ![]() , then the value of the expression
, then the value of the expression ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 2
Given the formula ![]() , then
, then ![]() equals to
equals to
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 3
A cyclist drives form town A to town B with velocity ![]() and comes back with velocity
and comes back with velocity ![]() . The mean velocity in
. The mean velocity in ![]() for the total distance is
for the total distance is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 4
We define the operation ![]() ,
, ![]() .
.
The value of ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 5
If the remainder of the division of ![]() with
with ![]() is
is ![]() , then the remainder of the division of
, then the remainder of the division of ![]() with
with ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 6
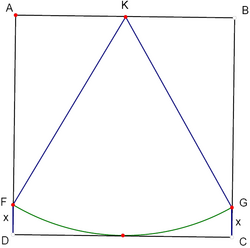
![]() is a square of side length 2 and
is a square of side length 2 and ![]() is an arc of the circle with centre the midpoint
is an arc of the circle with centre the midpoint ![]() of the side
of the side ![]() and radius 2. The length of the segments
and radius 2. The length of the segments ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
![]()
Problem 7
If a diagonal ![]() of a rectangle forms a
of a rectangle forms a ![]() angle with one of its sides, then the area of the rectangle is
angle with one of its sides, then the area of the rectangle is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 8
If we subtract from 2 the inverse number of ![]() , we get the inverse of
, we get the inverse of ![]() . Then the number
. Then the number ![]() equals to
equals to
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 9
We consider the sequence of real numbers ![]() such that
such that ![]() ,
, ![]() and
and ![]() ,
, ![]() . The value of the term
. The value of the term ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 10
The volume of an orthogonal parallelepiped is ![]() and its dimensions are integers. The minimum sum of the dimensions is
and its dimensions are integers. The minimum sum of the dimensions is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 11
If ![]() and
and ![]() , which of the following is correct?
, which of the following is correct?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 12
The function ![]() has the properties
has the properties ![]() and
and ![]()
![]() , where
, where ![]() is a constant. The value of
is a constant. The value of ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 13
If ![]() are the roots of the equation
are the roots of the equation ![]() and
and ![]() are the roots of the equation
are the roots of the equation ![]() , then the expression
, then the expression ![]() equals to
equals to
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 14
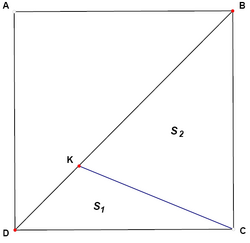
In the square ![]() the segment
the segment ![]() equals a side of the square. The ratio of areas
equals a side of the square. The ratio of areas ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 15
The reflex angles of the concave octagon ![]() measure
measure ![]() each. Diagonals
each. Diagonals ![]() and
and ![]() are perpendicular, bisect each other, and are both equal to
are perpendicular, bisect each other, and are both equal to ![]() .
.
The area of the octagon is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 16
The full time score of a football match was ![]() -
-![]() . how many possible half time results can we have for this match?
. how many possible half time results can we have for this match?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 17
The last digit of the number ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 18
How many subsets are there for the set ![]() ?
?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 19
120 five-digit numbers can be written with the digits ![]() . If we place these numbers in increasing order, then the position of the number
. If we place these numbers in increasing order, then the position of the number ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 20
The mean value for 9 Math-tests that a student succeded was ![]() (in scale
(in scale ![]() -
-![]() ). If we put the grades of these tests in incresing order, then the maximum grade of the
). If we put the grades of these tests in incresing order, then the maximum grade of the ![]() test is
test is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 21
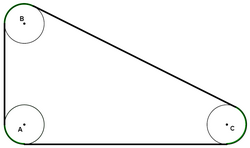
In the following figure, three equal cycles of diameter ![]() represent pulleys, that are connected with a strap. If the distances between any two pulley center points are
represent pulleys, that are connected with a strap. If the distances between any two pulley center points are ![]() ,
, ![]() and
and ![]() , then the length of the strap is
, then the length of the strap is
Α. ![]()
Β. ![]()
C. ![]()
D. ![]()
Ε. None of these
Problem 22
In the following figure ![]() is an orthogonal trapezium with $\ang A= \ang D=90^\circ$ (Error compiling LaTeX. Unknown error_msg) and bases
is an orthogonal trapezium with $\ang A= \ang D=90^\circ$ (Error compiling LaTeX. Unknown error_msg) and bases ![]() ,
, ![]() . If
. If ![]() and
and ![]() is the midpoint of the side
is the midpoint of the side ![]() , then
, then ![]() equals to
equals to
Α. ![]()
Β. ![]()
C. ![]()
D. ![]()
Ε. ![]()
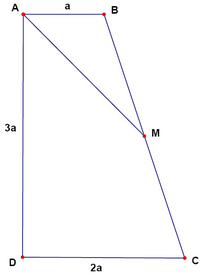
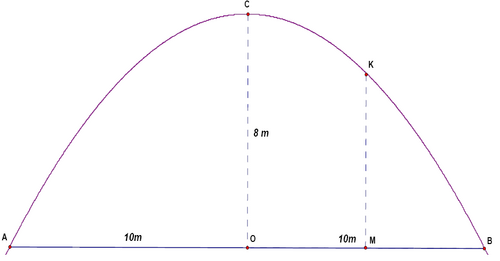
Problem 23
In the figure above the right section of a parabolic tunnel is presented. Its maximum height is ![]() and its maximum width is
and its maximum width is ![]() . If M is the midpoint of
. If M is the midpoint of ![]() , then the height
, then the height ![]() of the tunnel at the point
of the tunnel at the point ![]() is
is
Α. ![]()
Β. ![]()
C. ![]()
D. ![]()
Ε. ![]()
Problem 24
Costas sold two televisions for €198 each. From the sale of the first one he made a profit of 10% on its value and from the sale of the second one, he had a loss of 10% on its value. After the sale of the two televisions Costas had in total
A. profit €4
B. neither profit nor loss
C. loss €8
D. profit €8
E. loss €4
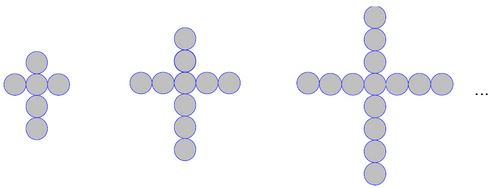
Problem 25
A jeweller makes crosses, according to the pattern shown above. The crosses are made from golden cyclical discs, with diameter of 1cm each. The height of a cross, which is made from 402 such discs is
Α. 198cm
Β. 2m
C. 201cm
D. 202cm
Ε. 204cm
Problem 26
The number of boys in a school is 3 times the number of girls and the number of girls is 9 times the number of teachers. Let us denote with ![]() ,
, ![]() and
and ![]() , the number of boys, girls and teachers respectively. Then the total number of boys, girls and teachers equals to
, the number of boys, girls and teachers respectively. Then the total number of boys, girls and teachers equals to
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 27
In the following diagram, the light beam ![]() is reflected on the
is reflected on the ![]() -axis and the beam
-axis and the beam ![]() , being reflected on a mirror parallel to the
, being reflected on a mirror parallel to the ![]() -axis at distance 6, intersects the
-axis at distance 6, intersects the ![]() -axis at point
-axis at point ![]() .
.
The equation of line ![]() is given by
is given by
Α. ![]()
Β. ![]()
C. ![]()
D. ![]()
Ε. ![]()
Problem 28
The product of ![]() is an integer number whose last digits are zeros. How many zeros are there?
is an integer number whose last digits are zeros. How many zeros are there?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 29
The minimum value of a positive integer ![]() , for which the sum
, for which the sum ![]() is a perfect square, is
is a perfect square, is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 30
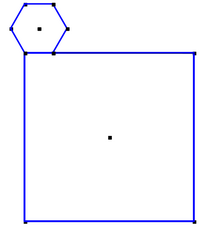
A coin with a shape of a regular hexagon of side 1 is tangent
to a square of side 6, as shown in the figure.
The coin rotates on the perimeter of the square, until it reaches
its original position.
The length of the line which is being inscribed by the centre of
the hexagon is
Α. ![]()
Β. ![]()
C. ![]()
D. ![]()
Ε. None of these