Difference between revisions of "2019 AMC 8 Problems/Problem 12"
Sum-of-sums (talk | contribs) m (→Solution 3) |
Holyangels (talk | contribs) m (→Solution 1) |
||
| Line 5: | Line 5: | ||
==Solution 1== | ==Solution 1== | ||
| − | <math>B</math> is on the top, and <math>R</math> is on the side, and <math>G</math> is on the right side. That means that (image <math>2</math>) <math>W</math> is on the left side. From the third image, you know that <math>P</math> must be on the bottom since <math>G</math> is sideways. That leaves us with the back, so the back must be <math>A</math>. The front is opposite of the back, so the answer is <math>\boxed{\textbf{(A)}\ R}</math>. | + | <math>B</math> is on the top, and <math>R</math> is on the side, and <math>G</math> is on the right side. That means that (image <math>2</math>) <math>W</math> is on the left side. From the third image, you know that <math>P</math> must be on the bottom since <math>G</math> is sideways. That leaves us with the back, so the back must be <math>A</math>. The front is opposite of the back, so the answer is <math>\boxed{\textbf{(A)}\ R}</math>. |
==Solution 2== | ==Solution 2== | ||
Revision as of 09:33, 25 February 2021
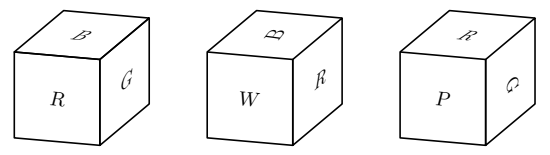
Problem
The faces of a cube are painted in six different colors: red ![]() , white
, white ![]() , green
, green ![]() , brown
, brown ![]() , aqua
, aqua ![]() , and purple
, and purple ![]() . Three views of the cube are shown below. What is the color of the face opposite the aqua face?
. Three views of the cube are shown below. What is the color of the face opposite the aqua face?
Solution 1
![]() is on the top, and
is on the top, and ![]() is on the side, and
is on the side, and ![]() is on the right side. That means that (image
is on the right side. That means that (image ![]() )
) ![]() is on the left side. From the third image, you know that
is on the left side. From the third image, you know that ![]() must be on the bottom since
must be on the bottom since ![]() is sideways. That leaves us with the back, so the back must be
is sideways. That leaves us with the back, so the back must be ![]() . The front is opposite of the back, so the answer is
. The front is opposite of the back, so the answer is ![]() .
.
Solution 2
Looking closely we can see that all faces are connected with ![]() except for
except for ![]() . Thus the answer is
. Thus the answer is ![]() .
.
It is A, just draw it out! ~phoenixfire
Solution 3
Associated video - https://www.youtube.com/watch?v=K5vaX_EzjEM
See also
| 2019 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
Only two of the cubes are required to solve the problem.