Difference between revisions of "1989 AIME Problems/Problem 12"
m |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
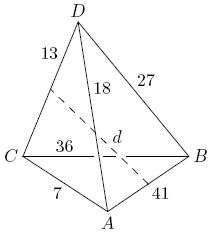
| + | Let <math>ABCD^{}_{}</math> be a tetrahedron with <math>AB=41^{}_{}</math>, <math>AC=7^{}_{}</math>, <math>AD=18^{}_{}</math>, <math>BC=36^{}_{}</math>, <math>BD=27^{}_{}</math>, and <math>CD=13^{}_{}</math>, as shown in the figure. Let <math>d^{}_{}</math> be the distance between the midpoints of edges <math>AB^{}_{}</math> and <math>CD^{}_{}</math>. Find <math>d^{2}_{}</math>. | ||
| + | |||
| + | [[Image:AIME_1989_Problem_12.png]] | ||
== Solution == | == Solution == | ||
| + | {{solution}} | ||
== See also == | == See also == | ||
| + | * [[1989 AIME Problems/Problem 13|Next Problem]] | ||
| + | * [[1989 AIME Problems/Problem 11|Previous Problem]] | ||
* [[1989 AIME Problems]] | * [[1989 AIME Problems]] | ||
Revision as of 22:18, 24 February 2007
Problem
Let 
be a tetrahedron with 
, 
, 
, 
, 
, and 
, as shown in the figure. Let 
be the distance between the midpoints of edges 
and 
. Find 
.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
