Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "User:Rowechen"

(→‎Problem 13)
Line 1: Line 1:
 
Here's the AIME compilation I will be doing:
 
Here's the AIME compilation I will be doing:
 +
== Problem 7 ==
 +
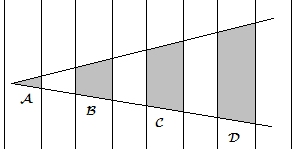
An angle is drawn on a set of equally spaced parallel lines as shown. The ratio of the area of shaded region <math> \mathcal{C} </math> to the area of shaded region <math> \mathcal{B} </math> is 11/5. Find the ratio of shaded region <math> \mathcal{D} </math> to the area of shaded region <math> \mathcal{A}.  </math>
  
−
==Problem 3==
+
[[Image:2006AimeA7.PNG]]
−
<math>x</math>, <math>y</math>, and <math>z</math> are positive integers. Let <math>N</math> denote the number of solutions of <math>2x + y + z = 2004</math>. Determine the remainder obtained when <math>N</math> is divided by <math>1000</math>.
 
  
 +
[[2006 AIME I Problems/Problem 7|Solution]]
 +
== Problem 2 ==
 +
A 100 foot long moving walkway moves at a constant rate of 6 feet per second.  Al steps onto the start of the walkway and stands.  Bob steps onto the start of the walkway two seconds later and strolls forward along the walkway at a constant rate of 2 feet per second.  Two seconds after that, Cy reaches the start of the walkway and walks briskly forward beside the walkway at a constant rate of 4 feet per second.  At a certain time, one of these three persons is exactly halfway between the other two.  At that time, find the distance in feet between the start of the walkway and the middle person.
  
−
==Problem 8==
+
[[2007 AIME I Problems/Problem 2|Solution]]
−
Find the number of sets <math>\{a,b,c\}</math> of three distinct positive integers with the property that the product of <math>a,b,</math> and <math>c</math> is equal to the product of <math>11,21,31,41,51,</math> and <math>61</math>.
+
== Problem 3 ==
 +
Let <math> P </math> be the product of the first 100 positive odd integers. Find the largest integer <math> k </math> such that <math> P </math> is divisible by <math> 3^k </math>.
  
−
[[2016 AIME II Problems/Problem 8 | Solution]]
+
[[2006 AIME II Problems/Problem 3|Solution]]
−
==Problem 9==
 
−
A special deck of cards contains <math>49</math> cards, each labeled with a number from <math>1</math> to <math>7</math> and colored with one of seven colors. Each number-color combination appears on exactly one card. Sharon will select a set of eight cards from the deck at random. Given that she gets at least one card of each color and at least one card with each number, the probability that Sharon can discard one of her cards and <math>\textit{still}</math> have at least one card of each color and at least one card with each number is <math>\frac{p}{q}</math>, where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>.
 
  
−
[[2017 AIME II Problems/Problem 9 | Solution]]
+
== Problem 9==
−
==Problem 7==
+
The value of the sum
 +
<cmath>\sum_{n=1}^{\infty} \frac{(7n+32)\cdot 3^n}{n\cdot(n+1)\cdot 4^n}</cmath>
 +
can be expressed in the form <math>\frac{p}{q}</math>, for some relatively prime positive integers <math>p</math> and <math>q</math>. Compute the value of <math>p + q</math>.
  
−
Triangle <math>ABC</math> has side lengths <math>AB = 12</math>, <math>BC = 25</math>, and <math>CA = 17</math>. Rectangle <math>PQRS</math> has vertex <math>P</math> on <math>\overline{AB}</math>, vertex <math>Q</math> on <math>\overline{AC}</math>, and vertices <math>R</math> and <math>S</math> on <math>\overline{BC}</math>. In terms of the side length <math>PQ = w</math>, the area of <math>PQRS</math> can be expressed as the quadratic polynomial
+
== Problem 8==
 +
Determine the remainder obtained when the expression
 +
<cmath>2004^{2003^{2002^{2001}}}</cmath>
 +
is divided by <math>1000</math>.
  
−
<cmath>\text{Area}(PQRS) = \alpha w - \beta \cdot w^2.</cmath>
+
==Problem 9==
−
 
+
Let
−
Then the coefficient <math>\beta = \frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
+
<cmath>(a+x^3)(a+2x^{3^2}) ... (1+kx^{3^k}) ... (1+1997x^{3^{1997}}) = 1+a_1x^{k_1}+a_2x^{k_2}+...+a_mx^{k_m}</cmath>
−
 
+
where <math>a_i \neq 0</math> and <math>k_1 < k_2 < ... < k_m</math>. Determine the remainder obtained when <math>a_1997</math> is divided by <math>1000</math>.
−
[[2015 AIME II Problems/Problem 7 | Solution]]
 
−
==Problem 7==
 
−
For integers <math>a</math> and <math>b</math> consider the complex number <cmath>\frac{\sqrt{ab+2016}}{ab+100}-\left(\frac{\sqrt{|a+b|}}{ab+100}\right)i.</cmath> Find the number of ordered pairs of integers <math>(a,b)</math> such that this complex number is a real number.
 
  
−
[[2016 AIME I Problems/Problem 7 | Solution]]
+
== Problem 11 ==
 +
A sequence is defined as follows <math> a_1=a_2=a_3=1, </math> and, for all positive integers <math> n, a_{n+3}=a_{n+2}+a_{n+1}+a_n. </math> Given that <math> a_{28}=6090307, a_{29}=11201821, </math> and <math> a_{30}=20603361, </math> find the remainder when <math>\sum^{28}_{k=1} a_k </math> is divided by 1000.
  
−
==Problem 8==
+
[[2006 AIME II Problems/Problem 11|Solution]]
−
A single atom of Uranium-238 rests at the origin. Each second, the particle has a <math>1/4</math> chance of moving one unit in the negative x-direction and a <math>1/2</math> chance of moving in the positive x-direction. If the particle reaches <math>(-3,0)</math>, it ignites fission that will consume the earth. If it reaches <math>(7, 0)</math>, it is harmlessly diffused. The probability that, eventually, the particle is safely contained can be expressed as <math>\frac{m}{n}</math> for some relatively prime positive integers <math>m</math> and <math>n</math>.
 
−
Determine the remainder obtained when <math>m + n</math> is divided by <math>1000</math>.
 
  
 
==Problem 10==
 
==Problem 10==
−
<math>ABCDE</math> is a cyclic pentagon with <math>BC = CD = DE</math>. The diagonals <math>AC</math> and <math>BE</math> intersect at <math>M</math>. <math>N</math> is the foot of the altitude from <math>M</math> to <math>AB</math>. We have <math>MA = 25</math>, <math>MD = 113</math>, and <math>MN = 15</math>. The area of triangle <math>ABE</math> can be expressed as <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Determine the remainder obtained when <math>m + n</math> is divided by <math>1000</math>.
+
<math>p, q</math>, and <math>r</math> are positive real numbers such that
−
 
+
<cmath>p^2+pq+q^2 = 211</cmath>
−
==Problem 12==
+
<cmath>q^2+qr+r^2 = 259</cmath>
 +
<cmath>r^2+rp+p^2 = 307</cmath>
 +
Compute the value of <math>pq + qr + rp</math>.
  
−
<math>ABCD</math> is a cyclic quadrilateral with <math>AB = 8</math>, <math>BC = 4</math>, <math>CD = 1</math>, and <math>DA = 7</math>. Let <math>O</math> and <math>P</math> denote the circumcenter and intersection of <math>AC</math> and <math>BD</math> respectively. The value of <math>OP^2</math> can be expressed as <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime, positive integers. Determine the remainder obtained when <math>m + n</math> is divided by <math>1000</math>.
 
 
==Problem 11==
 
==Problem 11==
−
For integers <math>a,b,c</math> and <math>d,</math> let <math>f(x)=x^2+ax+b</math> and <math>g(x)=x^2+cx+d.</math> Find the number of ordered triples <math>(a,b,c)</math> of integers with absolute values not exceeding <math>10</math> for which there is an integer <math>d</math> such that <math>g(f(2))=g(f(4))=0.</math>
+
<math>x_1</math>, <math>x_2</math>, and <math>x_3</math> are complex numbers such that
 +
<cmath>x_1 + x_2 + x_3 = 0</cmath>
 +
<cmath>x_1^2+x_2^2+x_3^2 = 16</cmath>
 +
<cmath>x_1^3+x_2^3+x_3^3 = -24</cmath>
  
−
[[2020 AIME I Problems/Problem 11 | Solution]]
+
Let <math>\gamma = min(|x1| , |x2| , |x3|)</math>, where <math>|a + bi| = \sqrt{a^2+b^2}</math>. Determine the value of <math>\gamma^6-15\gamma^4+\gamma^3+56\gamma^2</math>.
−
== Problem 10 ==
 
−
Seven teams play a soccer tournament in which each team plays every other team exactly once. No ties occur, each team has a <math> 50\% </math> chance of winning each game it plays, and the outcomes of the games are independent. In each game, the winner is awarded a point and the loser gets 0 points. The total points are accumulated to decide the ranks of the teams. In the first game of the tournament, team <math> A </math> beats team <math> B. </math> The probability that team <math> A </math> finishes with more points than team <math> B </math> is <math> m/n, </math> where <math> m </math> and <math> n </math> are relatively prime positive integers. Find <math> m+n. </math>
 
  
−
 
+
==Problem 12==
−
[[2006 AIME II Problems/Problem 10|Solution]]
+
<math>ABC</math> is a scalene triangle. The circle with diameter <math>AB</math> intersects <math>BC</math> at <math>D</math>, and <math>E</math> is the foot of the altitude from <math>C</math>. <math>P</math> is the intersection of <math>AD</math> and <math>CE</math>. Given that <math>AP = 136</math>, <math>BP = 80</math>, and <math>CP = 26</math>, determine the circumradius of <math>ABC</math>.
−
==Problem 14==
 
−
 
 
−
Centered at each lattice point in the coordinate plane are a circle radius <math>\frac{1}{10}</math> and a square with sides of length <math>\frac{1}{5}</math> whose sides are parallel to the coordinate axes. The line segment from <math>(0,0)</math> to <math>(1001, 429)</math> intersects <math>m</math> of the squares and <math>n</math> of the circles. Find <math>m + n</math>.
 
−
 
 
−
[[2016 AIME I Problems/Problem 14 | Solution]]
 
−
==Problem 15==
 
−
 
 
−
Circles <math>\omega_1</math> and <math>\omega_2</math> intersect at points <math>X</math> and <math>Y</math>. Line <math>\ell</math> is tangent to <math>\omega_1</math> and <math>\omega_2</math> at <math>A</math> and <math>B</math>, respectively, with line <math>AB</math> closer to point <math>X</math> than to <math>Y</math>. Circle <math>\omega</math> passes through <math>A</math> and <math>B</math> intersecting <math>\omega_1</math> again at <math>D \neq A</math> and intersecting <math>\omega_2</math> again at <math>C \neq B</math>. The three points <math>C</math>, <math>Y</math>, <math>D</math> are collinear, <math>XC = 67</math>, <math>XY = 47</math>, and <math>XD = 37</math>. Find <math>AB^2</math>.
 
−
 
 
−
[[2016 AIME I Problems/Problem 15 | Solution]]
 
−
 
 
−
==Problem 15==
 
−
<math>ABCD</math> is a convex quadrilateral in which <math>AB \parallel CD</math>. Let <math>U</math> denote the intersection of the extensions of <math>AD</math> and <math>BC</math>. <math>\Omega_1</math> is the circle tangent to line segment <math>BC</math> which also passes through <math>A</math> and <math>D</math>, and <math>\Omega_2</math> is the circle tangent to <math>AD</math> which passes through <math>B</math> and <math>C</math>. Call the points of tangency <math>M</math> and <math>S</math>. Let <math>O</math> and <math>P</math> be the points of intersection between <math>\Omega_1</math> and <math>\Omega_2</math>.
 
−
Finally, <math>MS</math> intersects <math>OP</math> at <math>V</math>. If <math>AB = 2</math>, <math>BC = 2005</math>, <math>CD = 4</math>, and <math>DA = 2004</math>, then the value of <math>UV^2</math> is some integer <math>n</math>. Determine the remainder obtained when <math>n</math> is divided by <math>1000</math>.
 
−
 
 
−
==Problem 13==
 
−
<math>P(x)</math> is the polynomial of minimal degree that satisfies
 
−
<cmath>P(k) = \frac{1}{k(k+1)}</cmath>
 
−
 
 
−
for <math>k = 1, 2, 3, . . . , 10</math>. The value of <math>P(11)</math> can be written as <math>-\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively
 
−
prime positive integers. Determine <math>m + n</math>.
 
−
 
 
−
==Problem 14==
 
−
<math>3</math> Elm trees, <math>4</math> Dogwood trees, and <math>5</math> Oak trees are to be planted in a line in front of a library such that
 
−
i) No two Elm trees are next to each other.
 
−
ii) No Dogwood tree is adjacent to an Oak tree.
 
−
iii) All of the trees are planted.
 
−
How many ways can the trees be situated in this manner?
 

Revision as of 18:29, 1 June 2020

Here's the AIME compilation I will be doing:

Problem 7

An angle is drawn on a set of equally spaced parallel lines as shown. The ratio of the area of shaded region $\mathcal{C}$ to the area of shaded region $\mathcal{B}$ is 11/5. Find the ratio of shaded region $\mathcal{D}$ to the area of shaded region $\mathcal{A}.$

2006AimeA7.PNG

Solution

Problem 2

A 100 foot long moving walkway moves at a constant rate of 6 feet per second. Al steps onto the start of the walkway and stands. Bob steps onto the start of the walkway two seconds later and strolls forward along the walkway at a constant rate of 2 feet per second. Two seconds after that, Cy reaches the start of the walkway and walks briskly forward beside the walkway at a constant rate of 4 feet per second. At a certain time, one of these three persons is exactly halfway between the other two. At that time, find the distance in feet between the start of the walkway and the middle person.

Solution

Problem 3

Let $P$ be the product of the first 100 positive odd integers. Find the largest integer $k$ such that $P$ is divisible by $3^k$.

Solution

Problem 9

The value of the sum \[\sum_{n=1}^{\infty} \frac{(7n+32)\cdot 3^n}{n\cdot(n+1)\cdot 4^n}\] can be expressed in the form $\frac{p}{q}$, for some relatively prime positive integers $p$ and $q$. Compute the value of $p + q$.

Problem 8

Determine the remainder obtained when the expression \[2004^{2003^{2002^{2001}}}\] is divided by $1000$.

Problem 9

Let \[(a+x^3)(a+2x^{3^2}) ... (1+kx^{3^k}) ... (1+1997x^{3^{1997}}) = 1+a_1x^{k_1}+a_2x^{k_2}+...+a_mx^{k_m}\] where $a_i \neq 0$ and $k_1 < k_2 < ... < k_m$. Determine the remainder obtained when $a_1997$ is divided by $1000$.

Problem 11

A sequence is defined as follows $a_1=a_2=a_3=1,$ and, for all positive integers $n, a_{n+3}=a_{n+2}+a_{n+1}+a_n.$ Given that $a_{28}=6090307, a_{29}=11201821,$ and $a_{30}=20603361,$ find the remainder when $\sum^{28}_{k=1} a_k$ is divided by 1000.

Solution

Problem 10

$p, q$, and $r$ are positive real numbers such that \[p^2+pq+q^2 = 211\] \[q^2+qr+r^2 = 259\] \[r^2+rp+p^2 = 307\] Compute the value of $pq + qr + rp$.

Problem 11

$x_1$, $x_2$, and $x_3$ are complex numbers such that \[x_1 + x_2 + x_3 = 0\] \[x_1^2+x_2^2+x_3^2 = 16\] \[x_1^3+x_2^3+x_3^3 = -24\]

Let $\gamma = min(|x1| , |x2| , |x3|)$, where $|a + bi| = \sqrt{a^2+b^2}$. Determine the value of $\gamma^6-15\gamma^4+\gamma^3+56\gamma^2$.

Problem 12

$ABC$ is a scalene triangle. The circle with diameter $AB$ intersects $BC$ at $D$, and $E$ is the foot of the altitude from $C$. $P$ is the intersection of $AD$ and $CE$. Given that $AP = 136$, $BP = 80$, and $CP = 26$, determine the circumradius of $ABC$.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=User:Rowechen&oldid=123445"