Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1983 AHSME Problems/Problem 17"

(Added a solution)
 
m (Added box at the bottom)
Line 15: Line 15:
  
 
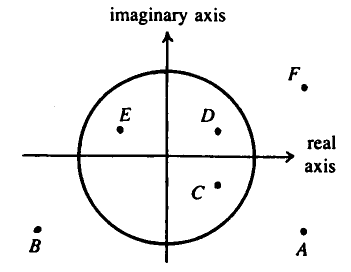
Write <math>F</math> as <math>a + bi</math>, where we see from the diagram that <math>a, b > 0</math> and <math>a^2+b^2>1</math> (<math>F</math> is outside the unit circle). We have <math>\frac{1}{a+bi} = \frac{a-bi}{a^2+b^2} = \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i</math>, so, since <math>a, b > 0</math>, the reciprocal of <math>F</math> has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of <math>F</math>'s magnitude (since <math>|a||b| = |ab|</math>); as <math>F</math>'s magnitude is greater than <math>1</math>, its reciprocal's magnitude will thus be between <math>0</math> and <math>1</math>, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of <math>F</math> is point <math>\boxed{\textbf{C}}</math>.
 
Write <math>F</math> as <math>a + bi</math>, where we see from the diagram that <math>a, b > 0</math> and <math>a^2+b^2>1</math> (<math>F</math> is outside the unit circle). We have <math>\frac{1}{a+bi} = \frac{a-bi}{a^2+b^2} = \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i</math>, so, since <math>a, b > 0</math>, the reciprocal of <math>F</math> has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of <math>F</math>'s magnitude (since <math>|a||b| = |ab|</math>); as <math>F</math>'s magnitude is greater than <math>1</math>, its reciprocal's magnitude will thus be between <math>0</math> and <math>1</math>, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of <math>F</math> is point <math>\boxed{\textbf{C}}</math>.
 +
 +
==See Also==
 +
{{AHSME box|year=1983|num-b=16|num-a=18}}
 +
 +
{{MAA Notice}}

Revision as of 23:55, 19 February 2019

Problem

Pdfresizer.com-pdf-convert-q17.png

The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin. One of these numbers is the reciprocal of $F$. Which one?

$\textbf{(A)} \ A \qquad \textbf{(B)} \ B \qquad \textbf{(C)} \ C \qquad \textbf{(D)} \ D \qquad \textbf{(E)} \ E$

Solution

Write $F$ as $a + bi$, where we see from the diagram that $a, b > 0$ and $a^2+b^2>1$ ($F$ is outside the unit circle). We have $\frac{1}{a+bi} = \frac{a-bi}{a^2+b^2} = \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i$, so, since $a, b > 0$, the reciprocal of $F$ has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of $F$'s magnitude (since $|a||b| = |ab|$); as $F$'s magnitude is greater than $1$, its reciprocal's magnitude will thus be between $0$ and $1$, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of $F$ is point $\boxed{\textbf{C}}$.

See Also

1983 AHSME (Problems • Answer Key • Resources)
Preceded by
Problem 16 		Followed by
Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
All AHSME Problems and Solutions


The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1983_AHSME_Problems/Problem_17&oldid=103573"