Difference between revisions of "1971 Canadian MO Problems/Problem 1"
(→Solution) |
(→Solution) |
||
| Line 6: | Line 6: | ||
== Solution == | == Solution == | ||
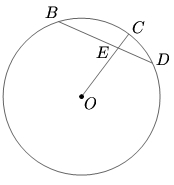
First, extend <math>CO</math> to meet the circle at <math>P.</math> Let the radius be <math>r.</math> Applying [[power of a point]], | First, extend <math>CO</math> to meet the circle at <math>P.</math> Let the radius be <math>r.</math> Applying [[power of a point]], | ||
| − | <math>( | + | <math>(EP)(CE)=(BE)(ED)</math> and <math>2r-1=15.</math> Hence, <math>r=8.</math> |
== See Also == | == See Also == | ||
Revision as of 22:49, 7 November 2018
Problem
is a chord of a circle such that 
and 
Let 
be the center of the circle. Join 
and extend to cut the circle at 
Given 
find the radius of the circle
Solution
First, extend 
to meet the circle at 
Let the radius be 
Applying power of a point,
and 
Hence, 
See Also
| 1971 Canadian MO (Problems) | ||
| Preceded by First Question |
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • | Followed by Problem 2 |
