Difference between revisions of "1961 AHSME Problems/Problem 11"
Rockmanex3 (talk | contribs) (Solution to Problem 11) |
Rockmanex3 (talk | contribs) (→Solution) |
||
| Line 12: | Line 12: | ||
==Solution== | ==Solution== | ||
| − | [[Image:1961 AHSME Problem 11.png| | + | [[Image:1961 AHSME Problem 11.png|300px|upright]] |
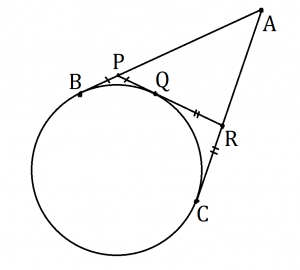
Draw the diagram as shown. Note that the two tangent lines from a single outside point of a circle have the exact same length, so <math>AB = AC = 20</math>, <math>BP = PQ</math>, and <math>QR = CR</math>. | Draw the diagram as shown. Note that the two tangent lines from a single outside point of a circle have the exact same length, so <math>AB = AC = 20</math>, <math>BP = PQ</math>, and <math>QR = CR</math>. | ||
Revision as of 11:06, 31 May 2018
Problem
Two tangents are drawn to a circle from an exterior point ![]() ; they touch the circle at points
; they touch the circle at points ![]() and
and ![]() respectively.
A third tangent intersects segment
respectively.
A third tangent intersects segment ![]() in
in ![]() and
and ![]() in
in ![]() , and touches the circle at
, and touches the circle at ![]() . If
. If ![]() , then the perimeter of
, then the perimeter of ![]() is
is
![]()
Solution
Draw the diagram as shown. Note that the two tangent lines from a single outside point of a circle have the exact same length, so ![]() ,
, ![]() , and
, and ![]() .
.
The perimeter of the triangle is ![]() . Note that
. Note that ![]() , so from substitution, the perimeter is
, so from substitution, the perimeter is
![]()
![]()
![]() Thus, the perimeter of the triangle is
Thus, the perimeter of the triangle is ![]() , so the answer is
, so the answer is ![]() .
.
See Also
| 1961 AHSC (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.