Difference between revisions of "2005 AMC 10A Problems/Problem 17"
(added diagram) |
m (fixed wording) |
||
| Line 9: | Line 9: | ||
Since each number is part of <math>2</math> numbers in the [[arithmetic sequence]], the sum of the arithmetic sequence is <math>2(3+5+6+7+9)=60</math> | Since each number is part of <math>2</math> numbers in the [[arithmetic sequence]], the sum of the arithmetic sequence is <math>2(3+5+6+7+9)=60</math> | ||
| − | Since the middle term in an arithmetic sequence is the average of the | + | Since the middle term in an arithmetic sequence is the average of all the terms in the sequence, the middle number is <math>\frac{60}{5}=12\Rightarrow D</math> |
==See Also== | ==See Also== | ||
Revision as of 16:41, 4 August 2006
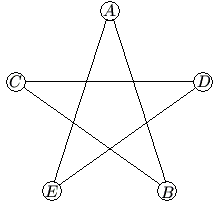
Problem
In the five-sided star shown, the letters 
, 
, 
, 
, and 
are replaced by the numbers 
, 
, 
, 
, and 
, although not necessarily in this order. The sums of the numbers at the ends of the line segments 
, 
, 
, 
, and 
form an arithmetic sequence, although not necessarily in this order. What is the middle term of the sequence?
Solution
Since each number is part of 
numbers in the arithmetic sequence, the sum of the arithmetic sequence is 
Since the middle term in an arithmetic sequence is the average of all the terms in the sequence, the middle number is 
