Difference between revisions of "Barycentric coordinates"
Mathletema (talk | contribs) |
Mathletema (talk | contribs) |
||
| Line 4: | Line 4: | ||
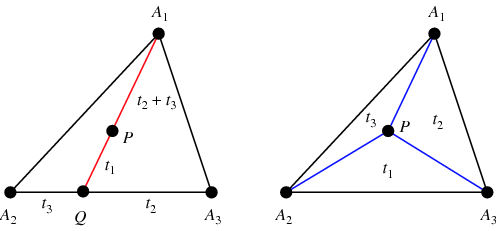
Barycentric coordinates are triples of numbers <math> (t_1,t_2,t_3) </math> corresponding to masses placed at the vertices of a reference triangle <math> \Delta{A_1}{A_2}{A_3} </math>. These masses then determine a point <math> P </math>, which is the geometric centroid of the three masses and is identified with coordinates <math> (t_1,t_2,t_3) </math>. The vertices of the triangle are given by <math> (1,0,0) </math>, <math> (0,1,0) </math>, and <math> (0,0,1) </math>. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993). | Barycentric coordinates are triples of numbers <math> (t_1,t_2,t_3) </math> corresponding to masses placed at the vertices of a reference triangle <math> \Delta{A_1}{A_2}{A_3} </math>. These masses then determine a point <math> P </math>, which is the geometric centroid of the three masses and is identified with coordinates <math> (t_1,t_2,t_3) </math>. The vertices of the triangle are given by <math> (1,0,0) </math>, <math> (0,1,0) </math>, and <math> (0,0,1) </math>. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993). | ||
| + | |||
| + | [[File:Barycentric_901.gif]] | ||
Revision as of 14:52, 5 February 2017
This can be used in mass points. http://mathworld.wolfram.com/BarycentricCoordinates.html This article is a stub. Help us out by expanding it.
Barycentric coordinates are triples of numbers 
corresponding to masses placed at the vertices of a reference triangle 
. These masses then determine a point 
, which is the geometric centroid of the three masses and is identified with coordinates . The vertices of the triangle are given by 
, 
, and 
. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
