Difference between revisions of "2011 AMC 10B Problems/Problem 25"
(→Solution) |
m (→Solution) |
||
| Line 53: | Line 53: | ||
triangle as <math>\frac{247}{256} + \frac{503}{256} < \frac{759}{256}</math>. | triangle as <math>\frac{247}{256} + \frac{503}{256} < \frac{759}{256}</math>. | ||
| − | Warning: This section is made by someone who is bad with LaTeX (aka TheUltimate123) | + | Warning: This section is made by someone who is bad with LaTeX (aka TheUltimate123). Please help with the LaTeX if any improvement is possible. Otherwise, delete this warning. Thanks! |
| − | |||
| − | |||
Likewise, you could create an equation instead of listing all the triangles to <math>T_{11}</math>. | Likewise, you could create an equation instead of listing all the triangles to <math>T_{11}</math>. | ||
The sides of a triangle <math>T_{k}</math> would be <math>\frac{503}{2^{k-3}} - 1, \frac{503}{2^{k-3}}, \frac{503}{2^{k-3}} + 1</math>. | The sides of a triangle <math>T_{k}</math> would be <math>\frac{503}{2^{k-3}} - 1, \frac{503}{2^{k-3}}, \frac{503}{2^{k-3}} + 1</math>. | ||
Revision as of 01:32, 22 January 2017
Problem
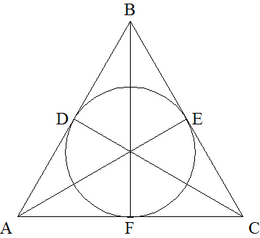
Let ![]() be a triangle with sides
be a triangle with sides ![]() and
and ![]() . For
. For ![]() , if
, if ![]() and
and ![]() and
and ![]() are the points of tangency of the incircle of
are the points of tangency of the incircle of ![]() to the sides
to the sides ![]() and
and ![]() respectively, then
respectively, then ![]() is a triangle with side lengths
is a triangle with side lengths ![]() and
and ![]() if it exists. What is the perimeter of the last triangle in the sequence
if it exists. What is the perimeter of the last triangle in the sequence ![]() ?
?
![]()
Solution
By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites.
Hence ![]() and
and ![]() and
and ![]() . Let
. Let ![]() and
and ![]() gives three equations:
gives three equations:
![]()
![]()
![]()
(where ![]() for the first triangle.)
for the first triangle.)
Solving gives:
![]()
![]()
![]()
Subbing in gives that ![]() has sides of
has sides of ![]() .
.
![]() can easily be derivied from this as the sides still differ by 1 hence the above solutions still work (now with
can easily be derivied from this as the sides still differ by 1 hence the above solutions still work (now with ![]() ). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
Subbing in gives ![]() with sides
with sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() would have sides
would have sides ![]() but these lengths do not make a
triangle as
but these lengths do not make a
triangle as ![]() .
.
Warning: This section is made by someone who is bad with LaTeX (aka TheUltimate123). Please help with the LaTeX if any improvement is possible. Otherwise, delete this warning. Thanks!
Likewise, you could create an equation instead of listing all the triangles to ![]() .
The sides of a triangle
.
The sides of a triangle ![]() would be
would be ![]() .
We then have
.
We then have ![]() .
Hence, the first triangle which does not exist in this sequence is
.
Hence, the first triangle which does not exist in this sequence is ![]() .
.
Hence the perimeter is ![]()
See Also
| 2011 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.