Difference between revisions of "Right triangle"
(add a bit, like usual needs revision) |
|||
| Line 6: | Line 6: | ||
Right triangles are very useful in [[geometry]] and for finding the [[area]]s of [[polygon]]s. The most important relationship for right triangles is the [[Pythagorean Theorem]]. In addition, the field of [[trigonometry]] arises from the study of right triangles, and nearly all [[trigonometric identities]] can be deduced from them. | Right triangles are very useful in [[geometry]] and for finding the [[area]]s of [[polygon]]s. The most important relationship for right triangles is the [[Pythagorean Theorem]]. In addition, the field of [[trigonometry]] arises from the study of right triangles, and nearly all [[trigonometric identities]] can be deduced from them. | ||
| + | |||
| + | == Special right triangles == | ||
| + | There are several well-known right triangles which are easy to solve. These include the [[isosceles triangle|isosceles]] <math>45-45-90</math>, where the hypotenuse is equal to <math>\sqrt{2}</math> times the length of either of the legs. The <math>30-60-90</math> has sides in the ratio of <math>x, x\sqrt{3}, 2x</math>. | ||
| + | |||
| + | If the lengths of the legs and hypotenuse are integral, then they form a [[Pythagorean triple]]. | ||
| + | |||
| + | == Properties == | ||
| + | The [[area]] of the triangle can be calculated using half of the product of the lengths of the legs. It can also be calculated using half of the product of the [[median]] to the hypotenuse and the hypotenuse. Using similarity, it is possible to derive several formulas relating the sides, the hypotenuse, and median. | ||
| + | |||
| + | == Problems == | ||
{{stub}} | {{stub}} | ||
Revision as of 21:31, 6 March 2007
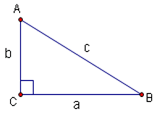
A right triangle is any triangle with an angle of 90 degrees (that is, a right angle).
In the image above, you see that in triangle 
, angle C has a measure of 90 degrees, so is a right triangle. The sides of a right triangle have different names: The longest side, opposite the right angle, is called the hypotenuse. In the diagram, the hypotenuse is labelled c. The other two sides are called the legs of the triangle.
Right triangles are very useful in geometry and for finding the areas of polygons. The most important relationship for right triangles is the Pythagorean Theorem. In addition, the field of trigonometry arises from the study of right triangles, and nearly all trigonometric identities can be deduced from them.
Special right triangles
There are several well-known right triangles which are easy to solve. These include the isosceles 
, where the hypotenuse is equal to 
times the length of either of the legs. The 
has sides in the ratio of 
.
If the lengths of the legs and hypotenuse are integral, then they form a Pythagorean triple.
Properties
The area of the triangle can be calculated using half of the product of the lengths of the legs. It can also be calculated using half of the product of the median to the hypotenuse and the hypotenuse. Using similarity, it is possible to derive several formulas relating the sides, the hypotenuse, and median.
Problems
This article is a stub. Help us out by expanding it.
