Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1987 AIME Problems/Problem 15"

(→‎Solution)
(→‎Solution)
Line 11: Line 11:
 
Setting the equations equal and solving for <math>T_5</math>, <math>T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}</math>. Therefore, <math>441T_5 = 441 + T_1 + T_2</math>. However, <math>441 + T_1 + T_2</math> is equal to the area of triangle <math>ABC</math>! This means that the ratio between the areas <math>T_5</math> and <math>ABC</math> is <math>441</math>, and the ratio between the sides is <math>\sqrt {441} = 21</math>. As a result, <math>AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}</math>. We now need <math>(AC)(BC)</math> to find the value of <math>AC + BC</math>, because <math>AB^2 + 2(AC)(BC) = (AC + BC)^2</math>.
 
Setting the equations equal and solving for <math>T_5</math>, <math>T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}</math>. Therefore, <math>441T_5 = 441 + T_1 + T_2</math>. However, <math>441 + T_1 + T_2</math> is equal to the area of triangle <math>ABC</math>! This means that the ratio between the areas <math>T_5</math> and <math>ABC</math> is <math>441</math>, and the ratio between the sides is <math>\sqrt {441} = 21</math>. As a result, <math>AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}</math>. We now need <math>(AC)(BC)</math> to find the value of <math>AC + BC</math>, because <math>AB^2 + 2(AC)(BC) = (AC + BC)^2</math>.
  
−
Let <math>h</math> denote the height to the [[hypotenuse]] of triangle <math>ABC</math>. Notice that <math>h - \frac {1}{21}h = \sqrt {440}</math>. (The height of <math>ABC</math> decreased by the corresponding height of <math>T_5</math>) Thus, <math>(AB)(h) = (AC)(BC) = 22\cdot 21^2</math>. Because <math>AB^2 + 2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2</math>, <math>AC + BC = (21)(22) = 462</math>.
+
Let <math>h</math> denote the height to the [[hypotenuse]] of triangle <math>ABC</math>. Notice that <math>h - \frac {1}{21}h = \sqrt {440}</math>. (The height of <math>ABC</math> decreased by the corresponding height of <math>T_5</math>) Thus, <math>(AB)(h) = (AC)(BC) = 22\cdot 21^2</math>. Because <math>AB^2 + 2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2</math>, <math>AC + BC = (21)(22) = \boxed{462}</math>.
  
 
== See also ==
 
== See also ==

Revision as of 18:16, 1 March 2016

Problem

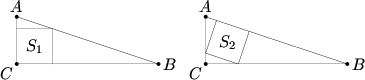
Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$, as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$.

AIME 1987 Problem 15.png

Solution

1987 AIME-15a.png

Because all the triangles in the figure are similar to triangle $ABC$, it's a good idea to use area ratios. In the diagram above, $\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.$ Hence, $T_3 = \frac {440}{441}T_1$ and $T_4 = \frac {440}{441}T_2$. Additionally, the area of triangle $ABC$ is equal to both $T_1 + T_2 + 441$ and $T_3 + T_4 + T_5 + 440.$

Setting the equations equal and solving for $T_5$, $T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}$. Therefore, $441T_5 = 441 + T_1 + T_2$. However, $441 + T_1 + T_2$ is equal to the area of triangle $ABC$! This means that the ratio between the areas $T_5$ and $ABC$ is $441$, and the ratio between the sides is $\sqrt {441} = 21$. As a result, $AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}$. We now need $(AC)(BC)$ to find the value of $AC + BC$, because $AB^2 + 2(AC)(BC) = (AC + BC)^2$.

Let $h$ denote the height to the hypotenuse of triangle $ABC$. Notice that $h - \frac {1}{21}h = \sqrt {440}$. (The height of $ABC$ decreased by the corresponding height of $T_5$) Thus, $(AB)(h) = (AC)(BC) = 22\cdot 21^2$. Because $AB^2 + 2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2$, $AC + BC = (21)(22) = \boxed{462}$.

See also

1987 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last
Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1987_AIME_Problems/Problem_15&oldid=77136"