Difference between revisions of "1992 AIME Problems/Problem 10"
(Undo revision 71030 by Starwars123 (talk)) |
(Undo revision 71029 by Starwars123 (talk)) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| + | |||
| + | == Solution == | ||
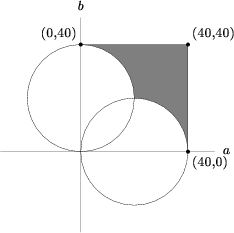
| + | Let <math>z=a+bi \implies \frac{z}{40}=\frac{a}{40}+\frac{b}{40}i</math>. Since <math>0\leq \frac{a}{40},\frac{b}{40}\leq 1</math> we have the inequality <cmath>0\leq a,b \leq 40</cmath>which is a square of side length <math>40</math>. | ||
| + | |||
| + | Also, <math>\frac{40}{\overline{z}}=\frac{40}{a-bi}=\frac{40a}{a^2+b^2}+\frac{40b}{a^2+b^2}i</math> so we have <math>0\leq a,b \leq \frac{a^2+b^2}{40}</math>, which leads to:<cmath>(a-20)^2+b^2\geq 20^2</cmath> | ||
| + | <cmath>a^2+(b-20)^2\geq 20^2</cmath> | ||
| + | |||
| + | We graph them: | ||
| + | |||
| + | <center>[[Image:AIME_1992_Solution_10.png]]</center> | ||
| + | |||
| + | We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is <math>40^2-\frac{40^2}{4}-\frac{1}{2}\pi 20^2\approx 571.68</math> | ||
<math>\boxed{572}</math> | <math>\boxed{572}</math> | ||
Revision as of 12:37, 8 July 2015
Problem
Solution
Let 
. Since 
we have the inequality ![\[0\leq a,b \leq 40\]](http://latex.artofproblemsolving.com/3/2/2/322dfb47bbc99f5371df34c835fbbfb8a0c07cba.png)
which is a square of side length 
.
Also, 
so we have 
, which leads to:![\[(a-20)^2+b^2\geq 20^2\]](http://latex.artofproblemsolving.com/a/2/a/a2abd8f5678c0cb9cebe1baf8ab5462cb46d6efc.png)
![\[a^2+(b-20)^2\geq 20^2\]](http://latex.artofproblemsolving.com/8/7/3/873e2f6de32b7d6432c3e28734d5ace419fd85ab.png)
We graph them:
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is 
