Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1989 AIME Problems/Problem 15"

(→‎Solution 2: Fixed LATEX rending being bad)
(→‎Solution 2: This solution is riddled with errors. I tried fixing some.)
Line 16: Line 16:
 
Using a different form of [[Ceva's Theorem]], we have <math>\frac {y}{x + y} + \frac {6}{6 + 6} + \frac {3}{3 + 9} = 1\Longleftrightarrow\frac {y}{x + y} = \frac {1}{4}</math>
 
Using a different form of [[Ceva's Theorem]], we have <math>\frac {y}{x + y} + \frac {6}{6 + 6} + \frac {3}{3 + 9} = 1\Longleftrightarrow\frac {y}{x + y} = \frac {1}{4}</math>
  
−
Solving <math>4y = x + y</math> and <math>x + y = 20</math>, we obtain <math>x = BP = 15</math> and <math>y = EP = 5</math>.
+
Solving <math>4y = x + y</math> and <math>x + y = 20</math>, we obtain <math>x = BP = 15</math> and <math>y = FP = 5</math>.
  
 
Let <math>Q</math> be the point on <math>AB</math> such that <math>FC \parallel QD</math>.
 
Let <math>Q</math> be the point on <math>AB</math> such that <math>FC \parallel QD</math>.
−
Since <math>AP = PD</math> and <math>FP\parallel QD</math>, <math>QD = 2FP = 6</math>. (Midline Theorem)
+
Since <math>AP = PD</math> and <math>FP\parallel QD</math>, <math>QD = 2FP = 10</math>. (Midline Theorem)
  
−
Also, since <math>FC\parallel QD</math> and <math>\QD = \frac{12}{FC}</math>, we see that <math>FQ = QB</math>, <math>BD = DC</math>, etc. ([[Midline Theorem]])
+
Also, since <math>FC\parallel QD</math> and <math>QD = \frac{FC}{2}</math>, we see that <math>FQ = QB</math>, <math>BD = DC</math>, etc. ([[Midline Theorem]])
 
Similarly, we have <math>PR = RB</math> (<math>= \frac12PB = 7.5</math>) and thus <math>RD = \frac12PC = 4.5</math>.
 
Similarly, we have <math>PR = RB</math> (<math>= \frac12PB = 7.5</math>) and thus <math>RD = \frac12PC = 4.5</math>.
  

Revision as of 22:44, 12 March 2015

Problem

Point $P$ is inside $\triangle ABC$. Line segments $APD$, $BPE$, and $CPF$ are drawn with $D$ on $BC$, $E$ on $AC$, and $F$ on $AB$ (see the figure below). Given that $AP=6$, $BP=9$, $PD=6$, $PE=3$, and $CF=20$, find the area of $\triangle ABC$.

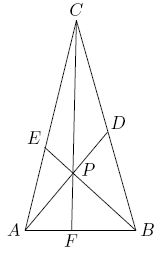
AIME 1989 Problem 15.png

Solution

Solution 1

Because we're given three concurrent cevians and their lengths, it seems very tempting to apply Mass points. We immediately see that $w_E = 3$, $w_B = 1$, and $w_A = w_D = 2$. Now, we recall that the masses on the three sides of the triangle must be balanced out, so $w_C = 1$ and $w_F = 3$. Thus, $CP = 15$ and $PF = 5$.

Recalling that $w_C = w_B = 1$, we see that $DC = DB$ and $DP$ is a median to $BC$ in $\triangle BCP$. Applying Stewart's Theorem, $BC^2 + 12^2 = 2(15^2 + 9^2)$, and $BC = 6\sqrt {13}$. Now notice that $2[BCP] = [ABC]$, because both triangles share the same base and the $h_{\triangle ABC} = 2h_{\triangle BCP}$. Applying Heron's formula on triangle $BCP$ with sides $15$, $9$, and $6\sqrt{13}$, $[BCP] = 54$ and $[ABC] = \boxed{108}$.

Solution 2

Using a different form of Ceva's Theorem, we have $\frac {y}{x + y} + \frac {6}{6 + 6} + \frac {3}{3 + 9} = 1\Longleftrightarrow\frac {y}{x + y} = \frac {1}{4}$

Solving $4y = x + y$ and $x + y = 20$, we obtain $x = BP = 15$ and $y = FP = 5$.

Let $Q$ be the point on $AB$ such that $FC \parallel QD$. Since $AP = PD$ and $FP\parallel QD$, $QD = 2FP = 10$. (Midline Theorem)

Also, since $FC\parallel QD$ and $QD = \frac{FC}{2}$, we see that $FQ = QB$, $BD = DC$, etc. (Midline Theorem) Similarly, we have $PR = RB$ ($= \frac12PB = 7.5$) and thus $RD = \frac12PC = 4.5$.

$PDR$ is a $3-4-5$ right triangle, so $\angle PDR$ ($\angle ADQ$) is $90^\circ$. Therefore, the area of $\triangle ADQ = \frac12\cdot 12\cdot 6 = 36$. Using area ratio, $\triangle ABC = \triangle ADB\times 2 = \left(\triangle ADQ\times \frac32\right)\times 2 = 36\cdot 3 = 108$.

Solution 3

Because the length of cevian $BE$ is unknown, we can examine what happens when we extend it or decrease its length and see that it simply changes the angles between the cevians. Wouldn't it be great if it the length of $BE$ was such that $\angle APC = 90^\circ$? Let's first assume it's a right angle and hope that everything works out.

Extend $AD$ to $Q$ so that $PD = DQ = 6$. The result is that $BQ = 9$, $PQ = 12$, and $BP = 15$ because $\triangle CDP\cong \triangle BDQ$. Now we see that if we are able to show that $BE = 20$, that is $PE = 5$, then our right angle assumption will be true.

Apply the Pythagorean Theorem on $\triangle APC$ to get $AC = 3\sqrt {13}$, so $AE = \sqrt {13}$ and $CE = 2\sqrt {13}$. Now, we apply the Law of Cosines on triangles $CEP$ and $AEP$.

Let $PE = x$. Notice that $\angle CEB = 180^\circ - \angle AEB$ and $\cos CEB = - \cos AEB$, so we get two nice equations.

$81 = 52 + y^2 - 2y \sqrt {13}\cos CEF$ $36 = 13 + y^2 + y \sqrt {13} \cos CEF$

Solving, $y = 5$ (yay!).

Now, the area is easy to find. $[ABC] = [AQB] + [APC] = \frac12(9)(18) + \frac12(6)(9) = 108$.

See also

1989 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Final Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1989_AIME_Problems/Problem_15&oldid=68790"