Difference between revisions of "1995 AIME Problems/Problem 9"
m |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
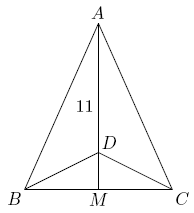
| + | Triangle <math>\displaystyle ABC</math> is isosceles, with <math>\displaystyle AB=AC</math> and altitude <math>\displaystyle AM=11.</math> Suppose that there is a point <math>\displaystyle D</math> on <math>\displaystyle \overline{AM}</math> with <math>\displaystyle AD=10</math> and <math>\displaystyle \angle BDC=3\angle BAC.</math> Then the perimeter of <math>\displaystyle \triangle ABC</math> may be written in the form <math>\displaystyle a+\sqrt{b},</math> where <math>\displaystyle a</math> and <math>\displaystyle b</math> are integers. Find <math>\displaystyle a+b.</math> | ||
| + | |||
| + | [[Image:AIME_1995_Problem_9.png]] | ||
== Solution == | == Solution == | ||
== See also == | == See also == | ||
| + | * [[1995_AIME_Problems/Problem_8|Previous Problem]] | ||
| + | * [[1995_AIME_Problems/Problem_10|Next Problem]] | ||
* [[1995 AIME Problems]] | * [[1995 AIME Problems]] | ||
Revision as of 00:21, 22 January 2007
Problem
Triangle 
is isosceles, with 
and altitude 
Suppose that there is a point 
on 
with 
and 
Then the perimeter of 
may be written in the form 
where 
and 
are integers. Find 
