Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2002 AIME I Problems"

 
Line 1: Line 1:
 
== Problem 1 ==
 
== Problem 1 ==
 +
Many states use a sequence of three letters followed by a sequence of three digits as their standard license-plate pattern. Given that each three-letter three-digit arrangement is equally likely, the probability that such a license plate will contain at least one palindrome (a three-letter arrangement or a three-digit arrangement that reads the same left-to-right as it does right-to-left) is <math>m/n</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
  
 
[[2002 AIME I Problems/Problem 1|Solution]]
 
[[2002 AIME I Problems/Problem 1|Solution]]
  
 
== Problem 2 ==
 
== Problem 2 ==
 +
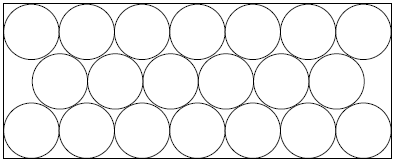
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as <math>\frac{1}{2}\left(\sqrt{p}-q\right)</math>, where <math>p</math> and <math>q</math> are positive integers. Find <math>p+q</math>.
 +
 +
<center>[[Image:AIME_2002I_Problem_02.png]]</center>
  
 
[[2002 AIME I Problems/Problem 2|Solution]]
 
[[2002 AIME I Problems/Problem 2|Solution]]
  
 
== Problem 3 ==
 
== Problem 3 ==
 +
Jane is 25 years old. Dick is older than Jane. In <math>n</math> years, where n is a positive integer, Dick's age and Jane's age will both be two-digit number and will have the property that Jane's age is obtained by interchanging the digits of Dick's age. Let <math>d</math> be Dick's present age. How many ordered pairs of positive integers <math>(d,n)</math> are possible?
  
 
[[2002 AIME I Problems/Problem 3|Solution]]
 
[[2002 AIME I Problems/Problem 3|Solution]]
  
 
== Problem 4 ==
 
== Problem 4 ==
 +
Consider the sequence defined by <math>a_k=\frac 1{k^2+k}</math> for <math>k\ge 1</math>. Given that <math>a_m+a_{m+1}+\cdots+a_{n-1}=1/29</math>, for positive integers <math>m</math> and <math>n</math> with <math>m<n</math>, find <math>m+n</math>.
  
 
[[2002 AIME I Problems/Problem 4|Solution]]
 
[[2002 AIME I Problems/Problem 4|Solution]]
  
 
== Problem 5 ==
 
== Problem 5 ==
 +
Let <math>A_1, A_2, A_3, \ldots, A_{12}</math> be the vertices of a regular dodecagon. How many distinct squares in the plane of the dodecagon have at least two vertices in the set <math>\{A_1,A_2,A_3,\ldots,A_{12}\}</math>?
  
 
[[2002 AIME I Problems/Problem 5|Solution]]
 
[[2002 AIME I Problems/Problem 5|Solution]]
  
 
== Problem 6 ==
 
== Problem 6 ==
 +
The solutions to the system of equations
 +
 +
<center><math>\begin{eqnarray*} \log_{225}{x}+\log_{64}{y} &=& 4\\ \log_x{225}-\log_y{64} &=& 1 \end{eqnarray*}</math></center>
 +
 +
are <math>(x_1,y_1)</math> and <math>(x_2, y_2)</math>. Find <math>\log_{30}{(x_1y_1x_2y_2)}</math>.
  
 
[[2002 AIME I Problems/Problem 6|Solution]]
 
[[2002 AIME I Problems/Problem 6|Solution]]
  
 
== Problem 7 ==
 
== Problem 7 ==
 +
The Binomial Expansion is valid for exponents that are not integers. That is, for all real numbers <math>x</math>, <math>y</math>, and <math>r</math> with <math>|x|>|y|</math>, <center><math>(x+y)^r=x^r+rx^{r-1}+\frac{r(r-1)}2x^{r-2}y^2+\frac{r(r-1)(r-2)}{3!}x^{r-3}y^3+\cdots</math></center>
 +
 +
What are the first three digits to the right of the decimal point in the decimal representation of <math>\left(10^{2002}+1\right)^{10/7}</math>?
  
 
[[2002 AIME I Problems/Problem 7|Solution]]
 
[[2002 AIME I Problems/Problem 7|Solution]]
  
 
== Problem 8 ==
 
== Problem 8 ==
 +
Find the smallest integer k for which the conditions
 +
 +
(1) <math>a_1, a_2, a_3, \ldots</math> is a nondecreasing sequence of positive integers
 +
 +
(2) <math>a_n=a_{n-1}+a_{n-2}</math> for all <math>n>2</math>
 +
 +
(3) <math>a_9=k</math>
 +
 +
are satisfied by more than one sequence.
  
 
[[2002 AIME I Problems/Problem 8|Solution]]
 
[[2002 AIME I Problems/Problem 8|Solution]]
  
 
== Problem 9 ==
 
== Problem 9 ==
 +
Harold, Tanya, and Ulysses paint a very long picket fence. Harold starts with the first picket and paints every <math>h</math>th picket; Tanya starts with the second picket and paints every <math>t</math>th picket; and Ulysses starts with the third picket and paints every <math>u</math>th picket. Call the positive integer <math>100h+10t+u</math> <math>\textit{paintable}</math> when the triple <math>(h,t,u)</math> of positive integers results in every picket being painted exactly once. Find the sum of all the paintable integers.
  
 
[[2002 AIME I Problems/Problem 9|Solution]]
 
[[2002 AIME I Problems/Problem 9|Solution]]
  
 
== Problem 10 ==
 
== Problem 10 ==
 +
In the diagram below, angle <math>ABC</math> is a right angle. Point <math>D</math> is on <math>\overline{BC}</math>, and <math>\overline{AD}</math> bisects angle <math>CAB</math>. Points <math>E</math> and <math>F</math> are on <math>\overline{AB}</math> and <math>\overline{AC}</math>, respectively, so that <math>AE=3</math> and <math>AF=10</math>. Given that <math>EB=9</math> and <math>FC=27</math>, find the integer closest to the area of quadrilateral <math>DCFG</math>.
 +
 +
<center>[[Image:AIME_2002I_Problem_10.png]]</center>
  
 
[[2002 AIME I Problems/Problem 10|Solution]]
 
[[2002 AIME I Problems/Problem 10|Solution]]
  
 
== Problem 11 ==
 
== Problem 11 ==
 +
Let <math>ABCD</math> and <math>BCFG</math> be two faces of a cube with <math>AB=12</math>. A beam of light emanates from vertex <math>A</math> and reflects off face <math>BCFG</math> at point <math>P</math>, which is <math>7</math> units from <math>\overline{BG}</math> and <math>5</math> units from <math>\overline{BC}</math>. The beam continues to be reflected off the faces of the cube. The length of the light path from the time it leaves point <math>A</math> until it next reaches a vertex of the cube is given by <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are integers and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>.
  
 
[[2002 AIME I Problems/Problem 11|Solution]]
 
[[2002 AIME I Problems/Problem 11|Solution]]
  
 
== Problem 12 ==
 
== Problem 12 ==
 +
Let <math>F(z)=\frac{z+i}{z-i}</math> for all complex numbers <math>z\not= i</math>, and let <math>z_n=F(z_{n-1})</math> for all positive integers <math>n</math>. Given that <math>z_0=\frac 1{137}+i</math> and <math>z_{2002}=a+bi</math>, where <math>a</math> and <math>b</math> are real numbers, find <math>a+b</math>.
  
 
[[2002 AIME I Problems/Problem 12|Solution]]
 
[[2002 AIME I Problems/Problem 12|Solution]]
  
 
== Problem 13 ==
 
== Problem 13 ==
 +
In triangle <math>ABC</math> the medians <math>\overline{AD}</math> and <math>\overline{CE}</math> have lengths 18 and 27, respectively, and <math>AB = 24</math>.  Extend <math>\overline{CE}</math> to intersect the circumcircle of <math>ABC</math> at <math>F</math>.  The area of traingle <math>AFB</math> is <math>m\sqrt {n}</math>, where <math>m</math> and <math>n</math> are positive integers and <math>n</math> is not divisible by the square of any prime.  Find <math>m + n</math>.
  
 
[[2002 AIME I Problems/Problem 13|Solution]]
 
[[2002 AIME I Problems/Problem 13|Solution]]
  
 
== Problem 14 ==
 
== Problem 14 ==
 +
A set <math>\mathcal{S}</math> of distinct positive integers has the following property: for every integer <math>x</math> in <math>\mathcal{S},</math> the arithmetic mean of the set of values obtained by deleting <math>x</math> from <math>\mathcal{S}</math> is an integer.  Given that 1 belongs to <math>\mathcal{S}</math> and that 2002 is the largest element of <math>\mathcal{S},</math> what is the greatet number of elements that <math>\mathcal{S}</math> can have?
  
 
[[2002 AIME I Problems/Problem 14|Solution]]
 
[[2002 AIME I Problems/Problem 14|Solution]]
  
 
== Problem 15 ==
 
== Problem 15 ==
 +
Polyhedron <math>ABCDEFG</math> has six faces.  Face <math>ABCD</math> is a square with <math>AB = 12;</math> face <math>ABFG</math> is a trapezoid with <math>\overline{AB}</math> parallel to <math>\overline{GF},</math> <math>BF = AG = 8,</math> and <math>GF = 6;</math> and face <math>CDE</math> has <math>CE = DE = 14.</math>  The other three faces are <math>ADEG, BCEF,</math> and <math>EFG.</math>  The distance from <math>E</math> to face <math>ABCD</math> is 12.  Given that <math>EG^2 = p - q\sqrt {r},</math> where <math>p, q,</math> and <math>r</math> are positive integers and <math>r</math> is not divisible by the square of any prime, find <math>p + q + r.</math>
  
 
[[2002 AIME I Problems/Problem 15|Solution]]
 
[[2002 AIME I Problems/Problem 15|Solution]]

Revision as of 14:07, 25 November 2007

Problem 1

Many states use a sequence of three letters followed by a sequence of three digits as their standard license-plate pattern. Given that each three-letter three-digit arrangement is equally likely, the probability that such a license plate will contain at least one palindrome (a three-letter arrangement or a three-digit arrangement that reads the same left-to-right as it does right-to-left) is $m/n$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Solution

Problem 2

The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as $\frac{1}{2}\left(\sqrt{p}-q\right)$, where $p$ and $q$ are positive integers. Find $p+q$.

AIME 2002I Problem 02.png

Solution

Problem 3

Jane is 25 years old. Dick is older than Jane. In $n$ years, where n is a positive integer, Dick's age and Jane's age will both be two-digit number and will have the property that Jane's age is obtained by interchanging the digits of Dick's age. Let $d$ be Dick's present age. How many ordered pairs of positive integers $(d,n)$ are possible?

Solution

Problem 4

Consider the sequence defined by $a_k=\frac 1{k^2+k}$ for $k\ge 1$. Given that $a_m+a_{m+1}+\cdots+a_{n-1}=1/29$, for positive integers $m$ and $n$ with $m<n$, find $m+n$.

Solution

Problem 5

Let $A_1, A_2, A_3, \ldots, A_{12}$ be the vertices of a regular dodecagon. How many distinct squares in the plane of the dodecagon have at least two vertices in the set $\{A_1,A_2,A_3,\ldots,A_{12}\}$?

Solution

Problem 6

The solutions to the system of equations

$\begin{eqnarray*} \log_{225}{x}+\log_{64}{y} &=& 4\\ \log_x{225}-\log_y{64} &=& 1 \end{eqnarray*}$ (Error compiling LaTeX. Unknown error_msg)

are $(x_1,y_1)$ and $(x_2, y_2)$. Find $\log_{30}{(x_1y_1x_2y_2)}$.

Solution

Problem 7

The Binomial Expansion is valid for exponents that are not integers. That is, for all real numbers $x$, $y$, and $r$ with $|x|>|y|$,

$(x+y)^r=x^r+rx^{r-1}+\frac{r(r-1)}2x^{r-2}y^2+\frac{r(r-1)(r-2)}{3!}x^{r-3}y^3+\cdots$

What are the first three digits to the right of the decimal point in the decimal representation of $\left(10^{2002}+1\right)^{10/7}$?

Solution

Problem 8

Find the smallest integer k for which the conditions

(1) $a_1, a_2, a_3, \ldots$ is a nondecreasing sequence of positive integers

(2) $a_n=a_{n-1}+a_{n-2}$ for all $n>2$

(3) $a_9=k$

are satisfied by more than one sequence.

Solution

Problem 9

Harold, Tanya, and Ulysses paint a very long picket fence. Harold starts with the first picket and paints every $h$th picket; Tanya starts with the second picket and paints every $t$th picket; and Ulysses starts with the third picket and paints every $u$th picket. Call the positive integer $100h+10t+u$ $\textit{paintable}$ when the triple $(h,t,u)$ of positive integers results in every picket being painted exactly once. Find the sum of all the paintable integers.

Solution

Problem 10

In the diagram below, angle $ABC$ is a right angle. Point $D$ is on $\overline{BC}$, and $\overline{AD}$ bisects angle $CAB$. Points $E$ and $F$ are on $\overline{AB}$ and $\overline{AC}$, respectively, so that $AE=3$ and $AF=10$. Given that $EB=9$ and $FC=27$, find the integer closest to the area of quadrilateral $DCFG$.

AIME 2002I Problem 10.png

Solution

Problem 11

Let $ABCD$ and $BCFG$ be two faces of a cube with $AB=12$. A beam of light emanates from vertex $A$ and reflects off face $BCFG$ at point $P$, which is $7$ units from $\overline{BG}$ and $5$ units from $\overline{BC}$. The beam continues to be reflected off the faces of the cube. The length of the light path from the time it leaves point $A$ until it next reaches a vertex of the cube is given by $m\sqrt{n}$, where $m$ and $n$ are integers and $n$ is not divisible by the square of any prime. Find $m+n$.

Solution

Problem 12

Let $F(z)=\frac{z+i}{z-i}$ for all complex numbers $z\not= i$, and let $z_n=F(z_{n-1})$ for all positive integers $n$. Given that $z_0=\frac 1{137}+i$ and $z_{2002}=a+bi$, where $a$ and $b$ are real numbers, find $a+b$.

Solution

Problem 13

In triangle $ABC$ the medians $\overline{AD}$ and $\overline{CE}$ have lengths 18 and 27, respectively, and $AB = 24$. Extend $\overline{CE}$ to intersect the circumcircle of $ABC$ at $F$. The area of traingle $AFB$ is $m\sqrt {n}$, where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $m + n$.

Solution

Problem 14

A set $\mathcal{S}$ of distinct positive integers has the following property: for every integer $x$ in $\mathcal{S},$ the arithmetic mean of the set of values obtained by deleting $x$ from $\mathcal{S}$ is an integer. Given that 1 belongs to $\mathcal{S}$ and that 2002 is the largest element of $\mathcal{S},$ what is the greatet number of elements that $\mathcal{S}$ can have?

Solution

Problem 15

Polyhedron $ABCDEFG$ has six faces. Face $ABCD$ is a square with $AB = 12;$ face $ABFG$ is a trapezoid with $\overline{AB}$ parallel to $\overline{GF},$ $BF = AG = 8,$ and $GF = 6;$ and face $CDE$ has $CE = DE = 14.$ The other three faces are $ADEG, BCEF,$ and $EFG.$ The distance from $E$ to face $ABCD$ is 12. Given that $EG^2 = p - q\sqrt {r},$ where $p, q,$ and $r$ are positive integers and $r$ is not divisible by the square of any prime, find $p + q + r.$

Solution

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2002_AIME_I_Problems&oldid=20240"