Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1986 AIME Problems/Problem 14"
m
 
Line 23: Line 23:
 
<cmath>\frac {1}{h^2} + \frac {1}{l^2} = \frac {40}{900}</cmath>
 
<cmath>\frac {1}{h^2} + \frac {1}{l^2} = \frac {40}{900}</cmath>
  
−
We see that <math>h = 15</math>, <math>l = 5</math>, <math>w = 10</math>. Therefore <math>V = 5 \cdot 10 \cdot 15 = 750</math>.
+
We see that <math>h = 15</math>, <math>l = 5</math>, <math>w = 10</math>. Therefore <math>V = 5 \cdot 10 \cdot 15 = \boxed{750}</math>
  
 
== See also ==
 
== See also ==

Latest revision as of 12:13, 22 July 2020

Problem

The shortest distances between an interior diagonal of a rectangular parallelepiped, $P$, and the edges it does not meet are $2\sqrt{5}$, $\frac{30}{\sqrt{13}}$, and $\frac{15}{\sqrt{10}}$. Determine the volume of $P$.

Solution

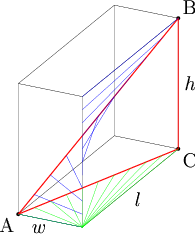
AIME 1986 Problem 14 sol.png

In the above diagram, we focus on the line that appears closest and is parallel to $BC$. All the blue lines are perpendicular lines to $BC$ and their other points are on $AB$, the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to $AC$, and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between $AC$ and that corner, which is $\frac {wl}{\sqrt {w^2 + l^2}}$.

So we have: \[\frac {lw}{\sqrt {l^2 + w^2}} = \frac {10}{\sqrt {5}}\] \[\frac {hw}{\sqrt {h^2 + w^2}} = \frac {30}{\sqrt {13}}\] \[\frac {hl}{\sqrt {h^2 + l^2}} = \frac {15}{\sqrt {10}}\]

Notice the familiar roots: $\sqrt {5}$, $\sqrt {13}$, $\sqrt {10}$, which are $\sqrt {1^2 + 2^2}$, $\sqrt {2^2 + 3^2}$, $\sqrt {1^2 + 3^2}$, respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)

\[\frac {l^2w^2}{l^2 + w^2} = \frac {1}{\frac {1}{l^2} + \frac {1}{w^2}} = 20\] \[\frac {h^2w^2}{h^2 + w^2} = \frac {1}{\frac {1}{h^2} + \frac {1}{w^2}} = \frac {900}{13}\] \[\frac {h^2l^2}{h^2 + l^2} = \frac {1}{\frac {1}{h^2} + \frac {1}{l^2}} = \frac {45}{2}\]

We invert the above equations to get a system of linear equations in $\frac {1}{h^2}$, $\frac {1}{l^2}$, and $\frac {1}{w^2}$: \[\frac {1}{l^2} + \frac {1}{w^2} = \frac {45}{900}\] \[\frac {1}{h^2} + \frac {1}{w^2} = \frac {13}{900}\] \[\frac {1}{h^2} + \frac {1}{l^2} = \frac {40}{900}\]

We see that $h = 15$, $l = 5$, $w = 10$. Therefore $V = 5 \cdot 10 \cdot 15 = \boxed{750}$

See also

1986 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1986_AIME_Problems/Problem_14&oldid=128865"