Difference between revisions of "Right triangle"
m (Right Triangle moved to Right triangle: not a proper noun) |
|||
| Line 1: | Line 1: | ||
| − | A right triangle is any triangle with an angle of 90 degrees. | + | A '''right triangle''' is any [[triangle]] with an angle of 90 degrees (that is, a [[right angle]]). |
[[Image:Righttriangle.png]] | [[Image:Righttriangle.png]] | ||
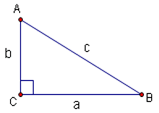
| − | In the | + | In the image above, you see that in triangle <math>\triangle ABC</math>, angle C has a measure of 90 degrees, so <math>\triangle ABC</math> is a right triangle. The sides of a right triangle have different names: The longest side, opposite the right angle, is called the [[hypotenuse]]. In the diagram, the hypotenuse is labelled c. The other two sides are called the legs of the triangle. |
| − | Right triangles are very useful in [[ | + | Right triangles are very useful in [[geometry]] and for finding the [[area]]s of [[polygon]]s. The most important relationship for right triangles is the [[Pythagorean Theorem]]. In addition, the field of [[trigonometry]] arises from the study of right triangles, and nearly all [[trigonometric identities]] can be deduced from them. |
| − | |||
| − | |||
| − | |||
| − | |||
{{stub}} | {{stub}} | ||
Revision as of 10:56, 17 July 2006
A right triangle is any triangle with an angle of 90 degrees (that is, a right angle).
In the image above, you see that in triangle 
, angle C has a measure of 90 degrees, so is a right triangle. The sides of a right triangle have different names: The longest side, opposite the right angle, is called the hypotenuse. In the diagram, the hypotenuse is labelled c. The other two sides are called the legs of the triangle.
Right triangles are very useful in geometry and for finding the areas of polygons. The most important relationship for right triangles is the Pythagorean Theorem. In addition, the field of trigonometry arises from the study of right triangles, and nearly all trigonometric identities can be deduced from them.
This article is a stub. Help us out by expanding it.
